Table of Contents
Traditional Materials
The orthotropic frame is a reference frame which is tied to the matter. It can be used to get stresses in a frame which is initially along given directions (for example, axial stresses on a sheet metal), or for anisotropic reasons. By default, the fame is aligned on the global one.
ElastHypoMaterial
Description
Basic elastic law.
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | |
| Young's modulus | ELASTIC_MODULUS | |
| Poisson Ratio | POISSON_RATIO | |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Objectivity Method (Jaumann = 0, GreenNaghdi = 1) | OBJECTIVITY | - |
| Orthotropic axis | ORTHO_AX1_X | - |
| Orthotropic axis | ORTHO_AX1_Y | - |
| Orthotropic axis | ORTHO_AX1_Z | - |
| Orthotropic axis | ORTHO_AX2_X | - |
| Orthotropic axis | ORTHO_AX2_Y | - |
| Orthotropic axis | ORTHO_AX2_Z | - |
| Orthotropic axis initialized by mesh construction boolean : True - False (def) override OrthoAxis definition | ORTHO_INIT_AS_JACO | - |
TmElastHypoMaterial
Description
Basic thermoelastic law
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | |
| Young's modulus | ELASTIC_MODULUS | |
| Poisson ratio | POISSON_RATIO | |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Objectivity method (Jaumann = 0, GreenNaghdi = 1) | OBJECTIVITY | - |
| Orthotropic axis | ORTHO_AX1_X | - |
| Orthotropic axis | ORTHO_AX1_Y | - |
| Orthotropic axis | ORTHO_AX1_Z | - |
| Orthotropic axis | ORTHO_AX2_X | - |
| Orthotropic axis | ORTHO_AX2_Y | - |
| Orthotropic axis | ORTHO_AX2_Z | - |
| Orthotropic axis initialized by mesh construction boolean : True - False (def) override OrthoAxis definition | ORTHO_INIT_AS_JACO | - |
| Thermal expansion | THERM_EXPANSION | TO/TM |
| Conductivity | CONDUCTIVITY | TO/TM |
| Heat capacity | HEAT_CAPACITY | TO/TM |
| Dissipated thermoelastic power fraction | DISSIP_TE | - |
| Dissipated (visco)plastic power fraction (Taylor-Quinney factor) | DISSIP_TQ | - |
KelvinVoigtViscoElastHypoMaterial
Description
The Kelvin-Voigt viscoelastic law result in adding a viscous effect on the elastic material.
The similar spring/damper model is shown at the figure below
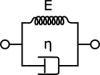
The effect of viscosity is only impacting deviatoric stresses (all computations done on a finite time step $\Delta t$)
$$ \begin{cases} p^{1} = p^{0} + 3K {\Delta\epsilon}_{ii} \\ s^{1}_{ij} = s^{0}_{ij} + 2G {\Delta\hat{\epsilon}}_{ij} + \eta \frac{{\Delta\hat{\epsilon}}_{ij}}{\Delta t} \end{cases} $$
where $K$ and $G$ are compressibility and shear modulus.
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | - |
| Young's modulus | ELASTIC_MODULUS | TO/TM |
| Poisson Ratio | POISSON_RATIO | TO/TM |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Viscosity coefficient | VISCO_ETA | TO/TM |
GeneralizedMaxwellViscoElastHypoMaterial
Description
The GeneralizedMaxwell viscoelastic model result in adding of up to now, maximum 2 visco-elastic Maxwell branches to the elastic material. The similar spring/damper model is shown at the figure below
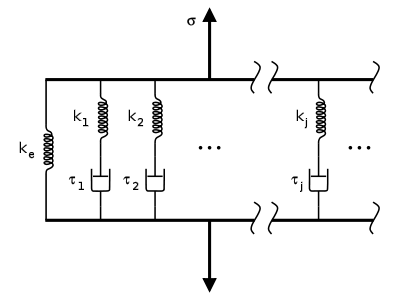
Defining Maxwell viscous parameters from materials data (for each Maxwell branch):
$$ \begin{cases} \Gamma_{i} &= \frac{\mu_{i}} {2G}\\ \tau_{i} &= \frac{\eta_{i}} {\mu_{i}} \end{cases} $$
The stresses in each Maxwell branch consist in 2 effects :
- the relaxation of previous time step stresses in this Maxwell branch
- the stress modification due to strain increment ${\Delta\epsilon}_{ij}$
$$ \begin{cases} p^{1} &= p^{0} + 3K {\Delta\epsilon}_{ii} \\ \underline{s}^{1} &= \underline{s}_{E}^{1} + \underline{s}^{1}_{M1} + \underline{s}^{1}_{M2} \end{cases} $$ Stresses in each branch are computed using : $$ \begin{cases} \underline{s}_{E}^{1} &= \underline{s}_{E}^{0} + 2G {\Delta\hat{\underline{\epsilon}}} \\ \underline{s}^{1}_{M1} &= e^{(\frac{-\Delta t}{\tau_{1}})} \underline{s}^{0}_{M1} + \Gamma_{1} (1-e^{\frac{-\Delta t}{\tau_{1}}}) \frac{\tau_{1}}{\Delta t} 2G {\Delta\hat{\underline{\epsilon}}} \\ \underline{s}^{1}_{M2} &= e^{(\frac{-\Delta t}{\tau_{2}})} \underline{s}^{0}_{M2} + \Gamma_{2} (1-e^{\frac{-\Delta t}{\tau_{2}}}) \frac{\tau_{2}}{\Delta t} 2G {\Delta\hat{\underline{\epsilon}}} \\ \end{cases} $$
where $K$ and $G$ are compressibility and shear modulus, ${\Delta\underline{\epsilon}}$ is the stain increment during the time step $\Delta t$. these equations shown clearly the necessity to track history of the total stresses but also to each Maxwell branch stresses $\underline{s}^{1}_{M1}$ and $\underline{s}^{1}_{M2}$.
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | - |
| Young's modulus | ELASTIC_MODULUS | TO/TM |
| Poisson Ratio | POISSON_RATIO | TO/TM |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Number of Maxwell branches 1 (default) or 2 | NBMAXWELLBRANCH | - |
| Maxwel 1 Stiffness | VISCO_MU1 | - |
| Maxwel 1 Viscosity | VISCO_ETA1 | - |
| Maxwel 2 Stiffness | VISCO_MU2 | - |
| Maxwel 2 Viscosity | VISCO_ETA2 | - |
model implemented based on Kaliske M, Rothert H. Formulation and implementation of three-dimensional viscoelasticity at small and finite strains. Computational Mechanics 1997;19:228-239.
EvpIsoHHypoMaterial
Description
Elasto-visco-plastic law with isotropic hardening (Yield Stress to define $ \sigma_{yield}$ ), imposed temperature.
Stresses are integrated with a radial return method. The stiffness tangent matrix is analytic and numerical.
The yield stress must verify the constraint:
$$ f=\overline{\sigma}-\sigma_{yield}=0 $$
where $ \overline{\sigma}$ is the equivalent stress computed as a function of the plastic criterion, and $ \sigma_{yield} $ is the yield stress.
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | - |
| Young's Modulus | ELASTIC_MODULUS | TM |
| Poisson Ratio | POISSON_RATIO | - |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Thermal Expansion | THERM_EXPANSION | TM |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Evolution law of the material temperature | TEMP | TM |
| Number of the plastic criterion (by default, it creates a VonMisesPlasticCriterion) | PLASTICCRITERION_NUM | - |
| Objectivity Method (Jaumann = 0, GreenNaghdi = 1) | OBJECTIVITY | - |
| Orthotropic axis | ORTHO_AX1_X | - |
| Orthotropic axis | ORTHO_AX1_Y | - |
| Orthotropic axis | ORTHO_AX1_Z | - |
| Orthotropic axis | ORTHO_AX2_X | - |
| Orthotropic axis | ORTHO_AX2_Y | - |
| Orthotropic axis | ORTHO_AX2_Z | - |
| Orthotropic axis initialized by mesh construction boolean : True - False (def) override OrthoAxis definition | ORTHO_INIT_AS_JACO | - |
TmEvpIsoHHypoMaterial
Description
Thermo-elasto-visco-plastic law with nonlinear isotropic hardening (no Hill48).
Stresses are integrated with a radial return method. The stiffness tangent matrix is analytic and numerical.
The yield stress must verify the constraint:
$$ f=\overline{\sigma}-\sigma_{yield}=0 $$
where $ \overline{\sigma}$ is the equivalent stress computed as a function of the Von Mises plastic criterion, and $ \sigma_{yield} $ is the yield stress.
Careful, here the TEMP parameter is not relevant anymore.

- When the thermal expansion changes, an average value is computed over the time step is estimated to model this thermal expansion properly.
- If the heat capacity changes, an average value is computed to estimate properly the energy balance. An equivalent heat capacity can be used to take into account the latent heat (= heat capacity + latent heat).
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | TO/TM |
| Young's Modulus | ELASTIC_MODULUS | TO/TM |
| Poisson Ratio | POISSON_RATIO | TO/TM |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Thermal expansion | THERM_EXPANSION | TO/TM |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Conductivity | CONDUCTIVITY | TO/TM |
| Heat capacity | HEAT_CAPACITY | TO/TM |
| Dissipated thermoelastic power fraction | DISSIP_TE | - |
| Dissipated (visco)plastic power fraction (Taylor-Quinney factor) | DISSIP_TQ | - |
EvpMixtHHypoMaterial
Description
Elasto-visco-plastic law with nonlinear isotropic mixed hardening (no Hill48), given temperature. The size of the plastic surface is defined by the Yield Stress.
Kinematic hardening are added to have a possibly quite complex resulting kinematic hardening. A maximum of five kinematic hardening laws are allowed (whether of the same type or a different one).
Stresses are integrated with a radial return method. The stiffness tangent matrix is analytic and numerical.
The yield stress must verify the constraint:
$$ f=\overline{\sigma}\left(\boldsymbol{\sigma},\boldsymbol{\alpha}\right)-\sigma_{yield}=0 $$
where $ \overline{\sigma} $ is the quivalent stress depending in the stress tensor $ \boldsymbol{\sigma} $ and of the backstresses $ \boldsymbol{\alpha} $, and where $ \sigma_{yield} $ is the Yield Stress.
Parameters (Metafor version <=3576)
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | - |
| Young's Modulus | ELASTIC_MODULUS | TM |
| Poisson Ratio | POISSON_RATIO | - |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Thermal expansion | THERM_EXPANSION | TM |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Number of kinematic hardening laws (maximum 5) | KH_NB | - |
| Number of kinematic hardening law 1 | KH_NUM1 | - |
| Number of kinematic hardening law 2 | KH_NUM2 | - |
| Number of kinematic hardening law 3 | KH_NUM3 | - |
| Number of kinematic hardening law 4 | KH_NUM4 | - |
| Number of kinematic hardening law 5 | KH_NUM5 | - |
| Material temperature evolution law | TEMP | TM |
Parameters (Metafor version >3576)
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | - |
| Young's Modulus | ELASTIC_MODULUS | TM |
| Poisson Ratio | POISSON_RATIO | - |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Thermal expansion | THERM_EXPANSION | TM |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Array of numbers defining the kinematic hardening laws ([1, 2,..]) | KH_NUMS | - |
| Material temperature evolution law | TEMP | TM |
TmEvpMixtHHypoMaterial
Description
This law, a thermomechanical elasto-visco-plastic law with mixed hardening, is the thermal version of the EvpMixtHHypoMaterial law. The thermal part of the law is identical to the one of the isotropic hardening law.
Physical parameters of the kinematic hardening laws can of course depend on the temperature.

- When the thermal expansion changes, an average value is computed over the time step is estimated to model this thermal expansion properly.
- If the heat capacity changes, an average value is computed to estimate properly the energy balance. An equivalent heat capacity can be used to take into account the latent heat (= heat capacity + latent heat).
Parameters (Metafor version <=3576)
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | TO/TM |
| Young's Modulus | ELASTIC_MODULUS | TO/TM |
| Poisson Ratio | POISSON_RATIO | TO/TM |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Thermal Expansion | THERM_EXPANSION | TO/TM |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Number of kinematic hardening laws (maximum 5) | KH_NB | - |
| Number of kinematic hardening law 1 | KH_NUM1 | - |
| Number of kinematic hardening law 2 | KH_NUM2 | - |
| Number of kinematic hardening law 3 | KH_NUM3 | - |
| Number of kinematic hardening law 4 | KH_NUM4 | - |
| Number of kinematic hardening law 5 | KH_NUM5 | - |
| Conductivity | CONDUCTIVITY | TO/TM |
| Heat Capacity | HEAT_CAPACITY | TO/TM |
| Dissipated thermoelastic power fraction | DISSIP_TE | - |
| Dissipated (visco)plastic power fraction (Taylor-Quinney factor) | DISSIP_TQ | - |
Parameters (Metafor version >3576)
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | TO/TM |
| Young's Modulus | ELASTIC_MODULUS | TO/TM |
| Poisson Ratio | POISSON_RATIO | TO/TM |
| Material Stiffness (STIFF_ANALYTIC - STIFF_NUMERIC) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Thermal Expansion | THERM_EXPANSION | TO/TM |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Array of numbers defining the kinematic hardening laws ([1, 2,..]) | KH_NUMS | - |
| Conductivity | CONDUCTIVITY | TO/TM |
| Heat Capacity | HEAT_CAPACITY | TO/TM |
| Dissipated thermoelastic power fraction | DISSIP_TE | - |
| Dissipated (visco)plastic power fraction (Taylor-Quinney factor) | DISSIP_TQ | - |
EvpIsoHDamageHypoMaterial
The EvpIsoHDamageHypoMaterial class manages Gurson damage. To create such a law, the class EvpIsoHDamageHypoMaterial must be derived with a function updateElasticProperties.
Description
EvpIsoHHypoMaterial law including Gurson damage (elasto-visco-plastic law with damage and nonlinear isotropic hardening (pas de Hill48), imposed temperature.
Stresses are integrated with a radial return method. The stiffness tangent matrix is analytic and numerical.
The yield stress must verify the constraint:
$$ f=\overline{\sigma}-w\left(D,p\right)\sigma_{yield}-\sigma_{damage}=0 $$
where $ \overline{\sigma} $ is the equivalent stress computed as a function of Von Mises plasticy criterion, $ \sigma_{yield} $ is the plastic stress updated as a function of the isotropic hardening, $ \omega $ is the reduction of the yield stress due to damage, $ D $ is the damage variable $p$ the pressure and $ \sigma_{damage} $ the stress associated to material damage.
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | |
| Young's Modulus | ELASTIC_MODULUS | |
| Poisson Ratio | POISSON_RATIO | |
| Material Stiffness (0 : Ana - 1 : Num) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Number of the damage evolution law | DAMAGE_NUM | |
| Initial damage | DAMAGE_INIT |
EvpIsoHDamageMoriTanakaHypoMaterial
The update of elastic properties is based on Mori-Tanaka law.
$$ G_d = \dfrac{G(1-d)}{1+d\frac{6K+12G}{9K+8G}} K_d = \dfrac{4GK(1-d)}{3Kd+4G} $$
EvpIsoHDamageJacobsHypoMaterial
if $d<0.43$
$$ G_d = G(1-d)^{3.2} K_d = G(1-d)^{3.2} $$
else
$$ G_d = Ga_0(1-d)^{2.5} K_d = Ga_0(1-d)^{2.5} $$ where $a_0=0.7$ by default
ContinuousDamageEvpIsoHHypoMaterial
Description
Elasto-visco-plastic law with continuous damage and nonlinear isotropic hardening (no Hill48), given temperature.
Stresses are integrated with a radial return method. The stiffness tangent matrix is analytic and numerical.
The yield stress must verify the constraint:
$$ f=\dfrac{\overline{\sigma}}{1-h\cdot D}-\sigma_{yield}=0 $$
where $ \overline{\sigma} $ is the equivalent stress computed as a function of Von Mises plasticy criterion, $ \sigma_{yield} $ is the yield stress, $ D $ is the damage variable updated as a function of the damage evolution law. Moreover, $h$ is the Micro-Crack Closure Effect parameter that makes the distinction of the weakening effect of damage under compressive and tensile stress states, which is defined as: $$ h = \left\{ \begin{array}{ll} \text{DAMAGE_MCCE} &\mbox{, if } \dfrac{p}{J_2}< 0.0\\ 1.0 &\mbox{, if } \dfrac{p}{J_2}\geq 0.0\\ \end{array} \right. $$
The evolution law coupled with plasticity can be integrated three ways depending on the parameter TYPE_INTEG:
TYPE_INTEG= 0 : iterative integration method (default)TYPE_INTEG= 1 : coupled integration methodTYPE_INTEG= 2 : integration method following the Souza algorithm
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | - |
| Young's Modulus | ELASTIC_MODULUS | TM |
| Poisson Ratio | POISSON_RATIO | - |
| Material Stiffness (0 : Ana - 1 : Num) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Number of the damage evolution law | DAMAGE_NUM | - |
| Initial damage | DAMAGE_INIT | - |
| Integration method | TYPE_INTEG | - |
| Micro-Crack Closure Effect parameter (=1.0 by default) | DAMAGE_MCCE |
ContinuousAnisoDamageEvpIsoHHypoMaterial
Description
Elasto-visco-plastic law with orthotropic damage and nonlinear isotropic hardening (no Hill48), given temperature.
Stresses are integrated with a radial return method. The stiffness tangent matrix is analytic and numerical.
The damage is a symmetric matrix $D$, the effective stress is computed from the stress tensor and from a fourth order tension $M$, which depends on $ H=(I-D)^{-1/2}$ and $ tr(D) $ : $ \tilde{\sigma}=M:\sigma$ and of $ \eta $, a parameter (double, at least equal to 1.0 - makes a material isotropic - usually taken as à 3.0 for traditional materials) (see Lemaitre, 2000 (equations 7 and 70) for information on $ M $).
The yield stress must verify the constraint:
$$ f=\overline{\sigma}_{eq}-\sigma_{yield}=0 $$
where $ \overline{\sigma}_{eq} $ is the equivalent stress computed as a function of Von Mises plasticy criterion (computed for $ \overline{\sigma} $ and not $ \sigma $), $ \sigma_{yield} $ is the yield stress.
$ H $ is the main damage variable, updated as a function of the damage evolution law.
The damage $D$ is initially diagonal.
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | - |
| Young's Modulus | ELASTIC_MODULUS | TM |
| Poisson Ratio | POISSON_RATIO | - |
| Material Stiffness (0 : Ana - 1 : Num) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Number of the damage evolution law | DAMAGE_NUM | - |
| Initial damage (11) | DAMAGE_INIT_1 | - |
| Initial damage (22) | DAMAGE_INIT_2 | - |
| Initial damage (33) | DAMAGE_INIT_3 | - |
| “weight” of the anisotropy, $ \eta $ | ETA | - |
TmContinuousDamageEvpIsoHHypoMaterial
Thermomechanical version of the material with continuous damage.

- When the thermal expansion changes, an average value is computed over the time step is estimated to model this thermal expansion properly.
- If the heat capacity changes, an average value is computed to estimate properly the energy balance. An equivalent heat capacity can be used to take into account the latent heat (= heat capacity + latent heat).
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Density | MASS_DENSITY | TO/TM |
| Young's Modulus | ELASTIC_MODULUS | TO/TM |
| Poisson Ratio | POISSON_RATIO | - |
| Material Stiffness (0 : Ana - 1 : Num) only if element Stiffness == STIFF_ANALYTIC | MATERIALSTIFFMETHOD | - |
| Number of the material law which defines the yield stress $\sigma_{yield}$ | YIELD_NUM | - |
| Number of the damage evolution law | DAMAGE_NUM | - |
| Initial damage | DAMAGE_INIT | - |
| Thermal Expansion | THERM_EXPANSION | TO/TM |
| Conductivity | CONDUCTIVITY | TO/TM |
| Heat Capacity | HEAT_CAPACITY | TO/TM |
| Dissipated thermoelastic power fraction | DISSIP_TE | - |
| Dissipated (visco)plastic power fraction (Taylor-Quinney factor) | DISSIP_TQ | - |
