Table of Contents
Yield Stress
The class YieldStress manages the yield stress used in the plastic criterion, whether plastic (isotropic hardening), visco-plastic (Perzyna as additive, Cowper-Symonds as multiplicative or ZerilliArmstrong, JohnsonCook, … as flow stress models)
$$ \sigma_{yield} = \sigma_{yield} (\bar{\varepsilon}^{vp}, \dot{\bar{\varepsilon}}^{vp}, grainSize, ...) $$
The laws implemented in Metafor are described below
IsotropicHardening
In order to simplify most of the test cases, the IsotropicHardening classes (Isotropic hardening) derive from the YieldStress class.
$$
\sigma_{yield} = \sigma_{isoHard}( \bar{\varepsilon}^{vp})
$$
Consequently, isotropic hardening is directly referred in the material as a YieldStress.
GsIsoHYieldStress
Yield Stress defined by an isotropic hardening:
$$ \sigma_{yield} = \sigma_{isoHard}( \bar{\varepsilon}^{vp}) + \sigma_{grainSize}( \bar{\varepsilon}^{vp}, \dot{\bar{\varepsilon}}^{vp}, grainSize ) $$
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Number of the isotropic hardening law | IH_NUM | |
| Number of the grain size evolution law | GS_NUM |
PerzynaYieldStress
Yield Stress defined by an isotropic hardening and a visco-plastic Perzyna yield stress:
$$ \sigma_{yield} = \sigma_{isoHard}( \bar{\varepsilon}^{vp}) + K (\dot{\bar{\varepsilon}}^{vp})^M \left(\bar{\varepsilon}^{vp}\right)^N $$
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Number of the isotropic hardening law | IH_NUM | |
| $K $ | PERZYNA_K | TM/TO |
| $M $ | PERZYNA_M | TM/TO |
| $N $ | PERZYNA_N | TM/TO |
GsPerzynaYieldStress
Yield Stress defined by an isotropic hardening, a visco-plastic Perzyna yield stress and a “grain size” stress:
$$ \sigma_{yield} = \sigma_{isoHard}( \bar{\varepsilon}^{vp}) + K (\dot{\bar{\varepsilon}}^{vp})^M \left(\bar{\varepsilon}^{vp}\right)^N + \sigma_{grainSize}( \bar{\varepsilon}^{vp}, \dot{\bar{\varepsilon}}^{vp}, grainSize ) $$
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Number of the isotropic hardening law | IH_NUM | |
| Number of the grain size evolution law | GS_NUM | |
| $K $ | PERZYNA_K | TM/TO |
| $M $ | PERZYNA_M | TM/TO |
| $N $ | PERZYNA_N | TM/TO |
JohnsonCookYieldStress
Johnson-Cook visco-plastic law:
\begin{multline} \sigma_{yield}= \left( A+B \left( \bar{\varepsilon}^{vp} \right)^n \right) \left(1+C\ln\left(\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)+C_2\left(\ln\left(\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)\right)^2\right) \\ \left( 1- \left( \dfrac{T-T_{room}}{T_{melt}-T_{room}} \right)^m \right) \end{multline}
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| $A $ | JC_A | TM/TO |
| $B $ | JC_B | TM/TO |
| $n $ | JC_N | TM/TO |
| $m $ | JC_M | TM/TO |
| Room temperature $T_{room}$ | JC_TROOM | TM/TO |
| Melting temperature $T_{melt}$ | JC_TMELT | TM/TO |
| $C $ | JC_C | TM/TO |
| $C_2 $ | JC_C2 | TM/TO |
| $\dot{\varepsilon}_0$ | JC_EPSP0 | TM/TO |
JohnsonCookMecYieldStress
Isotherm version of the Johnson-Cook visco-plastic law :
$$ \sigma_{yield}= \left( A+B \left( \bar{\varepsilon}^{vp} \right)^n \right) \left(1+C\ln\left(\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)+C_2\left(\ln\left(\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)\right)^2\right) $$
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| $A $ | JC_A | TM/TO |
| $B $ | JC_B | TM/TO |
| $n $ | JC_N | TM/TO |
| $C $ | JC_C | TM/TO |
| $C_2 $ | JC_C2 | TM/TO |
| ${\dot\varepsilon}_{0}$ | JC_EPSP0 | TM/TO |
PowJohnsonCookYieldStress
Power version of the Johnson-Cook visco-plastic law (PP implementation):
$$ \sigma_{yield}= \left( A+B \left( \bar{\varepsilon}^{vp} \right)^n \right) \left(1+\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)^C \left( 1- \left( \dfrac{T-T_{room}}{T_{melt}-T_{room}} \right)^m \right) $$
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| $A $ | JC_A | TM/TO |
| $B $ | JC_B | TM/TO |
| $n $ | JC_N | TM/TO |
| $m $ | JC_M | TM/TO |
| Room temperature $T_{room}$ | JC_TROOM | TM/TO |
| Melting temperature $T_{melt}$ | JC_TMELT | TM/TO |
| $C $ | JC_C | TM/TO |
| $\dot{\varepsilon}_0$ | JC_EPSP0 | TM/TO |
ZerilliArmstrongYieldStress
Zerilli-Armstong visco-plastic law:
$$ \sigma_{yield} = \sigma_0 + C_5 \left( \bar{\varepsilon}^{vp} \right) ^{n_1} + C_2 \left( \bar{\varepsilon}^{vp} \right)^{n_2} \exp \left( -C_3 T + C_4 T \ln \dot{\bar{\varepsilon}}^{vp} \right) $$
For FCC metals, $C_5=0$. For BCC metals, $n_2=0$.

Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| $\sigma_0$ | ZA_SIGMA0 | TM/TO |
| $C_5$ | ZA_C5 | TM/TO |
| $n_1$ | ZA_N1 | TM/TO |
| $C_2$ | ZA_C2 | TM/TO |
| $n_2$ | ZA_N2 | TM/TO |
| $C_3$ | ZA_C3 | TM/TO |
| $C_4$ | ZA_C4 | TM/TO |
CowperSymondsYieldStress
Cowper-Symonds visco-plastic law.
$$ \sigma_{yield}= \sigma_0 \left( 1 + \left(\dfrac{\dot{\overline{\varepsilon}}^{vp}}{D}\right)^{\frac{1}{p}} \right) $$
where $\sigma_0$ is the static yield stress, whose evolution is often given by a piecewise linear function.
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| Number of the hardening law | IH_NUM | |
| $D $ | CS_D | TM/TO |
| $p $ | CS_P | TM/TO |
ViscoKocksMeckingYieldStress
Description
Visco-plastic extension of the “Kocks-Mecking” isotropic hardening law.
$$ \sigma_{y} = \sigma_{y}^{0} + \sigma_{v} [1-exp(-\frac{\Theta_{0}}{\sigma_{v}} \bar{\varepsilon}^{vp}) ] \;\;\; si \;\;\; \sigma_{y} \leq \sigma_{y}^{tr} $$
$$ \sigma_{y} = \sigma_{y}^{tr} + \Theta_{IV} \left( \bar{\varepsilon}^{vp} - \bar{\varepsilon}^{vp}_{tr}\right) \;\;\; si \;\;\; \sigma_{y} > \sigma_{y}^{tr} $$
where $\sigma_{y}^{tr} $ is a transition yield stress, computed to guarantee continuity between both phases:
$$ \sigma_{y}^{tr} = \sigma_{y}^{0} + \sigma_{v}\frac{(\Theta_{0}-\Theta_{IV})}{\Theta_{0}} $$
and where $\bar{\varepsilon}^{vp}_{tr}$ is the corresponding plastic strain:
$$ \bar{\varepsilon}^{vp}_{tr} = \frac{\sigma_{v}}{\Theta_{0}} \ln \left(\frac{\Theta_{0}}{\Theta_{IV}}\right) $$
The viscous component of the yield stress is hidden in the calculation of the saturation stress:
$$ \sigma_{v} = \sigma_{v0} \left ( \frac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\bar{\varepsilon}}^{vp}_{0}} \right ) ^{\left (\frac{kT}{A} \right )} $$
$k$ : Boltzman's constant = $1.381e^{-23} \mbox{J}/\mbox{K}$
$T$ : Temperature K (CAREFUL in Kelvin : requires the definition of the temperature in the material)
$A$ : Activation energy (material constant)
${\dot{\bar{\varepsilon}}^{vp}_{0}}$ : reference plastic strain rate (= $1.e7$)
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| $\sigma_0$ | IH_SIGMA0 | TM/TO |
| $\Theta_{0}$ | KM_THETA0 | TM/TO |
| $\Theta_{IV}$ | KM_THETA4 | TM/TO |
| $\sigma_{v0}$ | KM_SIGV0 | - |
| ${\dot{\bar{\varepsilon}}^{vp}_{0}}$ | KM_DEVPL0 | - |
| $k$ : Boltzman's constant | KM_BOLTZMANN | - |
| $A$ | KM_A | - |
ViscoKocksMecking2YieldStress
Description
Second visco-plastic extension of the “Kocks-Mecking” isotropic hardening law, to match the Ta6V better.
No fourth step
The basic equation is still: $$ \sigma_{y} = \sigma_{y}^{0} + \sigma_{v} \left [1-exp \left (-\frac{\Theta_{0}}{\sigma_{v}} \bar{\varepsilon}^{vp}\right ) \right ] $$
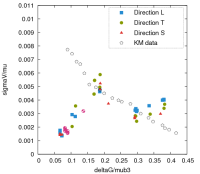
Both plastic strain rate and temperature dependency are hidden in the calculation of the Voce stress $\sigma_{v}$. If this Voce stress is plotted as a function of the $g$ parameter, defined as:
$$ g = \frac{kT}{\mu b^3} \ln \left ( \frac{\dot{\bar{\varepsilon}}^{vp}_{0}}{\dot{\bar{\varepsilon}}^{vp}} \right ) $$
where
$b$ : is the norm of the Burgers vector
$k$ : is the Boltzmann's constant
(for Ta6V, $ \frac{k}{b^3} ~ 1.135 $, in “$\mbox{Mpa}$”)
$T$ : Temperature K (CAREFUL in Kelvin : requires the definition of the temperature in the material)
$\mu$ : Elastic shear modulus of the material (requires a new definition of Young's modulus and Poisson ratio in the KM2 law!!!)
$\dot{\bar{\varepsilon}}^{vp}_{0}$: reference plastic strain rate (= $1.e7$)
the following figure is obtained:
KocksMecking usually predicts a linear evolution (KM data). However, the Ta6V trial data are the colored dots. The evolution is more in broken lines, defined as follow:
$G12$ and $G23$ are defined as the transition values between the three areas:
$$ \frac{\sigma_{v}}{\mu} = A1 \; g + B1 \;\;\;si\;\;\; g < G12 \\ \frac{\sigma_{v}}{\mu} = A2 \; g + B2 \;\;\;si\;\;\; G12 < g < G23 \\ \frac{\sigma_{v}}{\mu} = A3 \; g + B3 \;\;\;si\;\;\; G23 < g $$
Finally, the apparition of plasticity was observed to depend on strain rate and temperature (here, the temperature dependency is explicitly defined, but it could be done implicitly):
$$\sigma_0 = A + B T + (C + D T) \ln \left (\dot{\bar{\varepsilon}}^{vp}\right ) $$
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| $ A $ | IH_SIGEL_A | - |
| $ B $ | IH_SIGEL_B | - |
| $ C $ | IH_SIGEL_C | - |
| $ D $ | IH_SIGEL_D | - |
| $ A1 $ | KM2_SIGVOCE_A1 | - |
| $ B1 $ | KM2_SIGVOCE_B1 | - |
| $ G12 $ | KM2_SIGVOCE_G12 | - |
| $ A2 $ | KM2_SIGVOCE_A2 | - |
| $ B2 $ | KM2_SIGVOCE_B2 | - |
| $ G23 $ | KM2_SIGVOCE_G23 | - |
| $ A3 $ | KM2_SIGVOCE_A3 | - |
| $ B3 $ | KM2_SIGVOCE_B3 | - |
| $\frac{k}{b^3}$ | KM2_BOLTZMANN_BURGER3 | - |
| Young's Modulus | KM2_ELASTIC_MODULUS | - |
| Poisson ratio | KM2_POISSON_RATIO | - |
| $\Theta_{0}$ | KM_THETA0 | TM/TO |
| ${\dot{\bar{\varepsilon}}^{vp}_{0}}$ | KM_DEVPL0 | - |
SellarsTegartYieldStress
Yield Stress used for hot rolling defined by :
- a viscous power term :
$$ S0 = \sqrt{3} \; KK (\sqrt{3} \;\dot{\bar{\varepsilon}}^{vp})^{M0} $$
- a viscous asinh Term :
$$ Ss = As \; asinh((\frac{\dot{\bar{\varepsilon}}^{vp}}{Zs})^{Ms}) $$
- for the Yield Stress computed by (using a Voce hardening term):
$$ \sigma_{yield} = S0 + (Ss - S0) (1-e^{-C \; \bar{\varepsilon}^{vp}})^{R} $$
Parameters
| Name | Metafor Code | Dependency |
|---|---|---|
| $KK $ | SELLARSTEGART_KK | TM/TO |
| $M0 $ | SELLARSTEGART_M0 | TM/TO |
| $As $ | SELLARSTEGART_AS | TM/TO |
| $Zs $ | SELLARSTEGART_MS | TM/TO |
| $Ms $ | SELLARSTEGART_ZS | TM/TO |
| $C $ | SELLARSTEGART_R | TM/TO |
| $R $ | SELLARSTEGART_C | TM/TO |
PythonYieldStress
User defined Yield Stress by a pythonDirector : Python Director allows user to define their own Yield Stress law. Four functions has to be defined in the Python Class : a constructor (init), a destructor (del) that must never be called, and the computation functions : getYieldStress (returning YieldStress) and getYieldHardening (returning h). See the example below of a Perzyna law :
class MyYieldStress(PythonYieldStress):
def __init__(self, _no, _svm0, _h, _K, _m):
print("MyYieldStress: __init__")
PythonYieldStress.__init__(self,_no)
self.svm0 = _svm0
self.h = _h
self.K = _K
self.m = _m
def __del__(self):
print("MyIsoH : __del__")
print("callToDestructor of MyYieldStress not allowed. Add MyIsoH.__disown__()")
input('')
exit(1)
def getYieldStress(self, evpl, deltaEvpl, dTime, yieldGPState, pLaw):
#print "MyYieldStress compute Yield Stress"
if dTime > 0.0:
dEvpl = deltaEvpl/dTime
else:
dEvpl = 0.0
sigH = self.svm0+evpl*self.h
sigV = self.K*pow(dEvpl, self.m)
#yieldGPState.setVpStress(sigV)
return sigH+sigV
def getYieldHardening(self, epl, deltaEvpl, dTime, yieldGPState, pLaw) :
if dTime > 0.0:
dEvpl = deltaEvpl/dTime
h = self.h + (self.K*pow(dEvpl, self.m-1))/dTime
else:
dEvpl = 0.0
h = self.h
return h