This is an old revision of the document!
Table of Contents
Pressure and shear
Materials
Since pressure/shear interactions are boundary conditions interactions (LoadingInteraction), no materials must be associated to the element.
Element
Therefore, the first step consist in defining an ElementProperties, as
prp = ElementProperties(typeEl) prp.put(param1, value1) prp.depend(param1, fct1, Lock1)) #optional ...
where
typeEl | desired element (for example Traction[2|3]DElement) |
param1 | name of the property associated to the element (for example PRESSURE) |
value1 | value of the corresponding property |
fct1 | function which characterizes the dependency of the property (optional: no fct if no dependency) |
Lock1 | Lock which defines the dependency variable of the property (compulsory if there is a dependency) |
Traction2DElement, Traction3DElement
Traction/shear element for a mesh made of quadrangles in 2D or hexaedra in 3D.
Parameters
| Name | Description | Dependency |
|---|---|---|
STIFFMETHOD | Method used to compute the stiffness matrix = STIFF_ANALYTIC : analytic matrix (default)= STIFF_NUMERIC : numerical matrix | - |
PRESSURE | Pressure on the entity on which the propriety is applied | time |
SHEAR_KSI / SHEAR_ETA | Shear along $\xi$ or $\eta$ on the entity on which the propriety is applied | time |
NPG | Number of integration points (default : 2) | - |
ContactTraction2DElement, ContactTraction3DElement
Traction/shear element for a mesh made of quadrangles in 2D or hexaedra in 3D.
Parameters
| Name | Description | Dependency |
|---|---|---|
STIFFMETHOD | Method used to compute the stiffness matrix = STIFF_ANALYTIC : analytic matrix (default)= STIFF_NUMERIC : numerical matrix | - |
PRESSURE | Pressure on the entity on which the propriety is applied | time |
SHEAR_KSI / SHEAR_ETA | Shear along $\xi$ or $\eta$ on the entity on which the propriety is applied | time |
NPG | Number of integration points (default : 2) | - |
TriangleTraction3DElement
Traction/shear element for a mesh made of tetrahedra
Parameters
| Name | Description | Dependency |
|---|---|---|
STIFFMETHOD | Method used to compute the stiffness matrix\\= STIFF_ANALYTIC : analytic matrix (default)= STIFF_NUMERIC : numerical matrix Not applicable, only the numerical one exists ! | - |
PRESSURE | Pressure on the entity on which the propriety is applied | time |
SHEAR_KSI / SHEAR_ETA | Shear along $\xi$ or $\eta$ on the entity on which the propriety is applied | time |
NPG | Number of integration points (default : 1) | - |
Interaction
The interaction is defined as:
load = LoadingInteraction(no) load.push(gObject1) load.push(gObject2) ... load.addProperty(prp) interactionset.add(load)
where
no | number of the Interaction |
gObject1, gObject2 | meshed geometric entity where the boundary conditions are applied |
prp | Properties of boundary condition elements to generate |
Remark
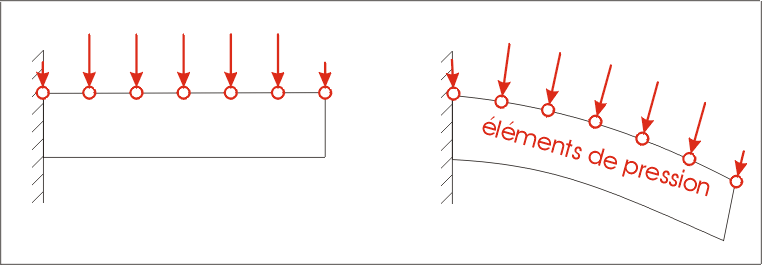
Traction, pressure and shear is generated by “traction elements”. Their definition requires a specific Interaction called LoadingInteraction, to which is associated an ElementProperties. These should not be mixed with dead loads. In most cases, traction elements should be chosen over dead loads:
- traction (or pressure/shear) is always defined in local axes, so the direction of the force depends on the orientation of the edge/face on which it is applied.
- traction is divided properly over all edges/faces on which the
Interactionis applied. Consequently, the resultant force does not depend on the mesh.