Metafor

Electrostatic painting is one of the applications I studied during my PhD. I started from a mathematical model by François Henrotte [1] and used this nice coupled problem to test different potential and mixed formulations of electrostatic equations.

The original device is made of a set of thin wires parallel to a grounded iron plate. The wires are brought to a negative potential of high amplitude. The strong electric field around the wires causes the acceleration of free electrons which move away from the cathode and combine with atoms. The negative ions drift toward the anode, i.e. the grounded plate, due to Coulomb forces. In the absence of coating particles, the system is described by classical electrostatic equations coupled with a transient convection equation, $$ \begin{eqnarray*} \nabla\cdot\vec{d} &=& \rho_i \\ \nabla\times\vec{e} &=& 0 \\ \vec{d} &=& \varepsilon_0\vec{e} \\ \partial_t \rho_i +\nabla\cdot( \mu_i\vec{e}\rho_i) &=& 0 \end{eqnarray*} $$ where $\mu_i$ is the ion mobility.

The convection equation is integrated in time with an implicit scheme and the electrostatic equations are solved at each time step. I implemented several electrostatic formulations to analyse their influence on the charge conservation: electric scalar potential ($\vec{e}=-\nabla V$), electric vector potential formulation with source field ($\vec{d}=\vec{d}_s+\nabla\times\vec{w}$) and mixed formulation ($\vec{d}$-$V$) [2]. It must be noted that electrostatic and magnetostatic mixed formulations have the same stability problems as Stokes equations when the shape functions do not satisfy the Babuska-Brezzi inf-sup condition. Fortunately, a stabilization technique developed in fluid mechanics, the so-called Pressure-Stabilized Petrov-Galerkin formulation, works fine with Maxwell's equations as well [3].

The geometrical model is a box extending from the middle of a wire to half the distance between two consecutive wires (Fig. 1). Fig. 2 shows the different fields of the vector potential formulation at the end of the simulation. The source field $\vec{d}_s$ is an arbitrary field such that $\nabla\cdot\vec{d}_s=\rho_i$. Fig. 3 (left) shows the currents flowing through the wire and the plate, which reach a steady state after 1.5ms approximately. In a real electrostatic painting problem, one should also model the flux of coating particles and their interactions with ions. Fig. 3 (right) shows that discretizing the electric displacement results in a better charge conservation than the classical scalar potential $V$ formulation, even if $V$ is discretized with second order shape functions.

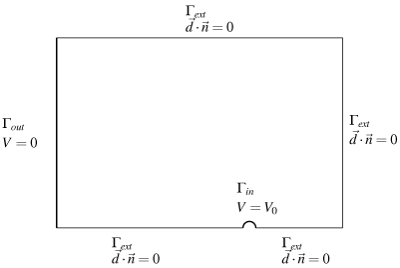Figure 1. Simplified geometry of the electrostatic painting device.

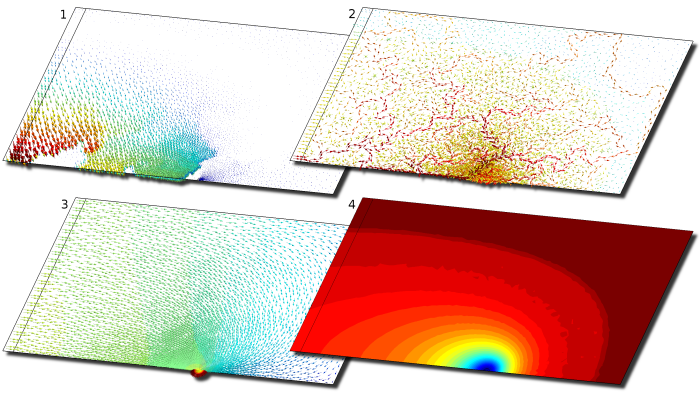Figure 2. Fields of the vector potential formulation at the end of the simulation (t=2ms): (1) vector potential $\vec{w}$, (2) source field $\vec{d}_s$, (3) electric displacement $\vec{d}=\vec{d}_s+\nabla\times\vec{w}$, (4) ion density $\rho_i$.

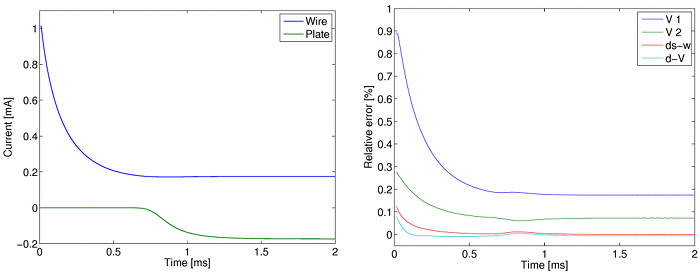Figure 3. Finite element simulation results : (left) current flowing through the wire and plate surfaces, (right) error on the charge conservation at each time step, calculated as the relative difference between the total charge variation during a time step and the integral of the currents on the wire and plate surfaces.

[1] F. Henrotte. Calcul des efforts électromagnétiques et de leurs effets dans des structures quelconques. PhD Thesis, Université de Liège, 2000
[2] G. Deliége, F. Henrotte, W. Deprez, K. Hameyer. Finite element modelling of ion convection by electrostatic forces. IET Science, Measurement & Technology, vol. 151, pp. 398-402, 2004
[3] G. Deliége, E. Rosseel, S. Vandewalle. Iterative solvers and stabilisation for mixed electrostatic and magnetostatic formulations. Journal of Computational & Applied Mathematics, vol. 215, pp. 348-356, 2008

Back to main page