Table of Contents
Commit 2015-11-18
Time Step Manager
Après quelques semaines de fouille et de patience, j'ai mis en place une structure pour la détermination du pas de temps au cours de l'intégration temporelle.
A titre informatif, nous prédisons d'abord le pas de temps du prochain pas sur base d'une méthode de calcul (Pas de temps critique, Nombre d'itérations NR, Erreur d'intégration temporelle) et ensuite il y a une possible correction du pas de temps suite à la valeur maximale du pas de temps prescrite sur la branche temporelle à intégrer et/ou la présence d'un archivage à un instant donné.
Afin d'ajouter la possibilité de faire une nouvelle méthode de calcul du pas de temps, une structure a été mise en place pour communiquer avec le Time Step Manager et avec d'autres objects (comme le Time Integration, Iteration Manager, Metafor, etc… pour aller chercher des informations sur la résolution du pas de temps).
La classe de base est TimeStepComputationMethod (classe virtuel pure). Afin d'éviter les structures en diamant (bad design) , je me suis inspiré de ce que l'on fait dans la visualisation graphique de Metafor. Ainsi, j'ai créé deux classes supplémentaires WithCriticalTimeStepEstimation et WithIntegrationErrorManager de base pour communiquer et pouvoir redéfinir des fonctions (ça évite aussi des références circulaires entre deux objets). Ainsi, par exemple, la classe CriticalTimeStepComputationMethod dérive de TimeStepComputationMethod et de WithCriticalTimeStepEstimation. Les objets relatifs à l'évaluation du pas de temps critique se trouve WithCriticalTimeStepEstimation. C'est la raison pour laquelle nous avons autant de nouveau objets.
Time Step Computation Method
Lors de mon refactoring, j'en ai profité pour faire un nettoyage des différentes classes visitées.
Pas de temps constant
Il est possible de faire l'intégration temporelle avec un pas de temps constant :
tscm = ConstantTimeStepComputationMethod(metafor) tsm.setTimeStepComputationMethod(tscm)
Remarques importantes :
- Si les itérations de la procédure de Newton Raphson ne convergent pas ou si il y a un jacobien négatif, nous avons l'arrêt de l'intégration temporelle au pas de temps donné !
- Cette méthode peut être utilisée avec tous les types de schéma d'intégration de Metafor.
- On peut préciser un pas de temps initial et un pas de temps maximal différent pour la branche d'intégration temporelle entre t0 et t1.
Pas de temps critique
Il est possible de faire l'intégration temporelle avec pas de temps déterminée à partir du pas de temps critique :
tscm = CriticalTimeStepComputationMethod(metafor) tscm.setExplicitTimeStepSecurity(_explicitTimeStepSecurity) tscm.setNbOfStepsForCriticalTimeStepUpdate(_nbOfStepsForCriticalTimeStepUpdate) tsm.setTimeStepComputationMethod(tscm)
Si les itérations NR ne convergent pas ou si il y a un jacobien négatif, nous avons l'arrêt de l'intégration temporelle à ce step là !
Nombre d'itérations de la procédure itérative de Newton Raphson
Il est possible de faire l'intégration temporelle avec pas de temps déterminé à partir du nombre d'itérations de la procédure itérative de Newton Raphson.
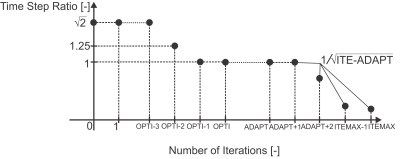
Le pas de temps est mis à jour sur base d'un nombre d'itérations optimal. Si le nombre d'itérations dépasse cette valeur, le pas de temps de diminué. Dans le cas contraire, le pas de temps est augmenté.
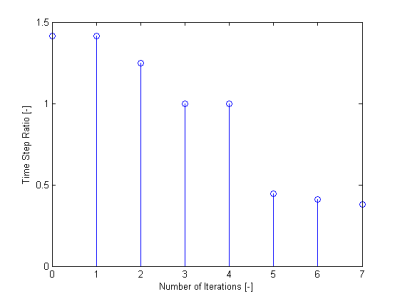
Voici une représentation schématique des deux algorithmes disponibles :
Voici deux exemples :
On distincte les différents cas suivants :
Schéma d'intégration mécanique
Le nombre d'itérations correspond au nombre d'itérations mécaniques :
tscm = NbOfMechNRIterationsTimeStepComputationMethod(metafor) tscm.setTimeStepDivisionFactor(_timeStepDivisionFactor) tscm.setMinimumTimeStep(_minimumTimeStep) tscm.setMaxNbOfIteInAdaptOfTimeStep(_maxNbOfIteInAdaptOfTimeStep) tscm.setNbOptiIte(_nbOptiIte) tsm.setTimeStepComputationMethod(tscm)
Schéma d'intégration thermo-mécanique étagé
Le nombre d'itérations correspond au maximum entre les nombres d'itérations mécaniques et thermiques :
tscm = NbOfStaggeredTmNRIterationsTimeStepComputationMethod(metafor) tscm.setTimeStepDivisionFactor(_timeStepDivisionFactor) tscm.setMinimumTimeStep(_minimumTimeStep) tscm.setMaxNbOfIteInAdaptOfTimeStep(_maxNbOfIteInAdaptOfTimeStep) tscm.setNbOptiIte(_nbOptiIte) tsm.setTimeStepComputationMethod(tscm)
Schéma d'intégration thermo-mécanique couplé
Le nombre d'itérations correspond au nombre d'itérations thermomécaniques :
tscm = NbOfCoupledTmNRIterationsTimeStepComputationMethod(metafor) tscm.setTimeStepDivisionFactor(_timeStepDivisionFactor) tscm.setMinimumTimeStep(_minimumTimeStep) tscm.setMaxNbOfIteInAdaptOfTimeStep(_maxNbOfIteInAdaptOfTimeStep) tscm.setNbOptiIte(_nbOptiIte) tsm.setTimeStepComputationMethod(tscm)
Schéma d'intégration mécanique avec Lagrangien Augmenté
Le nombre d'itérations correspond au nombre d'itérations mécaniques à l'augmentation n°0 :
tscm = NbOfAugLagMechNRIterationsTimeStepComputationMethod(metafor) tscm.setTimeStepDivisionFactor(_timeStepDivisionFactor) tscm.setMinimumTimeStep(_minimumTimeStep) tscm.setMaxNbOfIteInAdaptOfTimeStep(_maxNbOfIteInAdaptOfTimeStep) tscm.setNbOptiIte(_nbOptiIte) tsm.setTimeStepComputationMethod(tscm)
Erreur d'intégration temporelle
Il est possible de faire l'intégration temporelle avec un pas de temps déterminé à partir de l'erreur d'intégration temporelle du pas courant.
Le pas de temps courant est résolu jusqu'à ce que l'erreur d'intégration temporelle soit inférieure à celle prescrite. Si ce n'est pas le cas, le pas de temps est refusé et le pas de temps est recommencé avec un pas de temps tel que l'erreur d'intégration temporelle soit égale à celle prescrite.
Si le pas de temps est accepté, on diminue, on garde, ou on augmente le pas de temps sur base de la valeur de l'erreur d'intégration temporelle.
On distincte les différents cas suivants :
Schéma d'intégration quasi-statique
tscm = QuasiStaticIntegrationErrorTimeStepComputationMethod(metafor) tscm.setTimeStepDivisionFactor(_timeStepDivisionFactor) tscm.setMinimumTimeStep(_minimumTimeStep) tscm.setInitialIntegrationErrorTolerance(_initialIntegrationErrorTolerance) tsm.setTimeStepComputationMethod(tscm)
Schéma d'intégration explicite
tscm = ExplicitIntegrationErrorTimeStepComputationMethod(metafor) tscm.setInitialIntegrationErrorTolerance(_initialIntegrationErrorTolerance) tscm.setInitialExplicitTimeStepSecurity(_initialExplicitTimeStepSecurity) tscm.setNbOfStepsForCriticalTimeStepUpdate(_nbOfStepsForCriticalTimeStepUpdate) tsm.setTimeStepComputationMethod(tscm)
Schéma d'intégration implicite
tscm = IeIntegrationErrorTimeStepComputationMethod(metafor) tscm.setTimeStepDivisionFactor(_timeStepDivisionFactor) tscm.setMinimumTimeStep(_minimumTimeStep) tscm.setInitialIntegrationErrorTolerance(_initialIntegrationErrorTolerance) tsm.setTimeStepComputationMethod(tscm)
Schéma d'intégration implicite/explicite
tscm = IeIntegrationErrorTimeStepComputationMethod(metafor) tscm.setTimeStepDivisionFactor(_timeStepDivisionFactor) tscm.setMinimumTimeStep(_minimumTimeStep) tscm.setInitialIntegrationErrorTolerance(_initialIntegrationErrorTolerance) tscm.setInitialExplicitTimeStepSecurity(_initialExplicitTimeStepSecurity) tscm.setNbOfStepsForCriticalTimeStepUpdate(_nbOfStepsForCriticalTimeStepUpdate) tsm.setTimeStepComputationMethod(tscm)
Remarques importantes :
- Ces méthodes de mise à jour du pas de temps n'ont pas été testées dans le cas d'un schéma d'intégration thermo-mécanique !
- Si il y a un jacobien négatif durant un pas de temps, nous avons l'arrêt de l'intégration temporelle à ce pas de temps là dans le cas du schéma d'intégration explicite !
Paramètres
| Paramètre | Défaut | Description |
|---|---|---|
maxNbOfIteInAdaptOfTimeStep | 0 | Nombre d'itérations maximales pour faire diminuer le pas de temps si le nombre d'itérations est supérieur au nombre d'itérations optimales |
nbOptiIte | 4 | Nombre d'itérations optimales |
timeStepDivisionFactor | 3.0 | Facteur de division du pas de temps en cas de problème durant la résolution du step |
minimumTimeStep | 1.0E-10 | Pas de temps en dessous duquel on arrête l'intégration temporelle |
initialIntegrationErrorTolerance | 1.0E-4 | Erreur normalisée d'intégration temporelle initiale |
initialExplicitTimeStepSecurity | 2.0/3.0 | Facteur de sécurité initial du pas de temps critique |
nbOfStepsForCriticalTimeStepUpdate | 1 | Nombre de pas de temps entre chaque mise à jour du pas de temps critique |
Méthode par défaut de chaque schéma d'intégration
| Intégration temporelle | Défaut |
|---|---|
Quasi-statique Mechanical Time Integration | “NbOfMechNRIterationsTimeStepComputationMethod” |
Implicit Mechanical Time Integration | “NbOfMechNRIterationsTimeStepComputationMethod” |
Explicit Mechanical Time Integration | “CriticalTimeStepComputationMethod” |
Combined Implicit/Explicit Mechanical Time Integration | “IeIntegrationErrorTimeStepComputationMethod” |
Coupled ThermoMechanical Time Integration | “NbOfCoupledTmNRIterationsTimeStepComputationMethod” |
Staggered ThermoMechanical Time Integration | “NbOfStaggeredTmNRIterationsTimeStepComputationMethod” |
Divers
Il y a toujours les points nébuleux suivants :
Integration Error
Il y a pas mal de lignes de code sans documentation (Articles, Thèses, …) qui servent à éviter une augmentation ou une diminution trop forte du pas de temps, ainsi que pour limiter le pas de temps lorsqu'il y a eu un pas de temps avec une non-convergence des itérations.
Détermination du pas de temps critique
Malgré ma documentation sur le sujet, je ne suis pas sur du tout que l'on calcule correctement le pas de temps critique par la méthode itérative de la puissance selon Benson et surtout dans le cas des matériaux visco-élastiques ou des matériaux avec des propriétés élastiques dépendent du temps !
Automatic IeShiftManager
Il y a pas mal de lignes de code sans documentation (Articles, Thèses, …) qui servent à éviter un basculement du schéma d'intégration trop fréquent de l'implicite vers l'explicite ou l'inverse.
Cas Tests
Pas de temps constant
J'ai ajouté une version du cas test cont2.py avec un pas de temps constant.
Modifications
Le schéma d'intégration du cas test apps/qs/cylBarNeckQuadQuad.py est désormais quasi-statique.
Fichiers/Dossiers ajoutés/supprimés
[a]:mtFEM/algos/AdaptativeTimeStepComputationMethod.cpp [a]:mtFEM/algos/AdaptativeTimeStepComputationMethod.h [a]:mtFEM/algos/ConstantTimeStepComputationMethod.cpp [a]:mtFEM/algos/ConstantTimeStepComputationMethod.h [a]:mtFEM/algos/CriticalTimeStepComputationMethod.cpp [a]:mtFEM/algos/CriticalTimeStepComputationMethod.h [a]:mtFEM/algos/CriticalTimeStepEstimation.cpp [a]:mtFEM/algos/CriticalTimeStepEstimation.h [a]:mtFEM/algos/ExplicitIntegrationErrorTimeStepComputationMethod.cpp [a]:mtFEM/algos/ExplicitIntegrationErrorTimeStepComputationMethod.h [a]:mtFEM/algos/IeIntegrationErrorTimeStepComputationMethod.cpp [a]:mtFEM/algos/IeIntegrationErrorTimeStepComputationMethod.h [a]:mtFEM/algos/ImplicitIntegrationErrorTimeStepComputationMethod.cpp [a]:mtFEM/algos/ImplicitIntegrationErrorTimeStepComputationMethod.h [a]:mtFEM/algos/NbOfAugLagMechNRIterationsTimeStepComputationMethod.cpp [a]:mtFEM/algos/NbOfAugLagMechNRIterationsTimeStepComputationMethod.h [a]:mtFEM/algos/NbOfCoupledTmNRIterationsTimeStepComputationMethod.cpp [a]:mtFEM/algos/NbOfCoupledTmNRIterationsTimeStepComputationMethod.h [a]:mtFEM/algos/NbOfMechNRIterationsTimeStepComputationMethod.cpp [a]:mtFEM/algos/NbOfMechNRIterationsTimeStepComputationMethod.h [a]:mtFEM/algos/NbOfStaggeredTmNRIterationsTimeStepComputationMethod.cpp [a]:mtFEM/algos/NbOfStaggeredTmNRIterationsTimeStepComputationMethod.h [a]:mtFEM/algos/NbOfTherNRIterationsTimeStepComputationMethod.cpp [a]:mtFEM/algos/NbOfTherNRIterationsTimeStepComputationMethod.h [a]:mtFEM/algos/QuasiStaticIntegrationErrorTimeStepComputationMethod.cpp [a]:mtFEM/algos/QuasiStaticIntegrationErrorTimeStepComputationMethod.h [a]:mtFEM/algos/TimeStepComputationMethod.cpp [a]:mtFEM/algos/TimeStepComputationMethod.h [a]:mtFEM/algos/WithCriticalTimeStepEstimation.cpp [a]:mtFEM/algos/WithCriticalTimeStepEstimation.h [a]:mtFEM/algos/WithIntegrationErrorManager.cpp [a]:mtFEM/algos/WithIntegrationErrorManager.h [rename]: mtFEM/algos/CriticalTimeStep.cpp => mtFEM/algos/CriticalTimeStepEstimationByPowerIteration.cpp [rename]: mtFEM/algos/CriticalTimeStep.h => mtFEM/algos/CriticalTimeStepEstimationByPowerIteration.h [rename]: mtFEM/algos/NbOfIterationsTimeStepComputationMethod.cpp => mtFEM/algos/NbOfNRIterationsTimeStepComputationMethod.cpp [rename]: mtFEM/algos/NbOfIterationsTimeStepComputationMethod.h => mtFEM/algos/NbOfNRIterationsTimeStepComputationMethod.h
Tests ajoutés/supprimés
[r]: [a]:apps/qs/cont2ConstantTimeStep.py [rename]: apps/qs/CylBarNeckQuadQuad.py => apps/qs/cylBarNeckQuadQuad.py
— Gaëtan WAUTELET 2015/11/18