The general feature of this commit is described in the first section, then the corresponding test case, and finally, some minor modifications.

In this commit, the out-of-plane thickness evolution in the generalized plane strain state is coherently accounted for in the computation. Previously, the possible increase or decrease of the out-of-plane thickness via the depend command was not taken into account in the contact area computation. This led to an incoherently changing gap in the following scenario, where AIC_ONCEPERSTEP is activated.

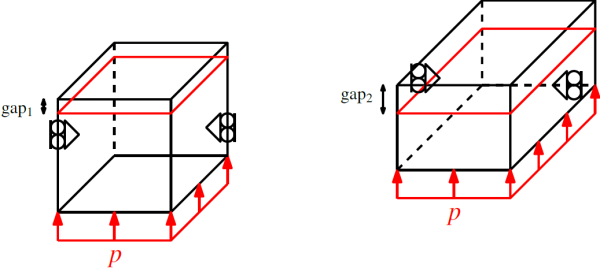
In the previous figure, the square is represented in 3D although the computation is performed in the generalized plane strain state. The lateral movement of the left and right sides of the square is blocked. A pressure $p$, identical in both cases, pushes the square against the contact tool (frictionless). When the out-of-plane thickness of the square increases, as shown on the right, the resultant force created by the pressure increases due to the increase of the surface on which this pressure is applied. Moreover, if the increase of the out-of-plane thickness is not taken into account in the contact interaction, i.e. in the computation of the area in contact, the increase of the resultat pressure force will increase the gap. Hence, $\text{gap}_{1} < \text{gap}_{2}$ previously. In the new version, $\text{gap}_{1} = \text{gap}_{2}$. In fact, the gap should remain constant, if the contact pressure remains constant.

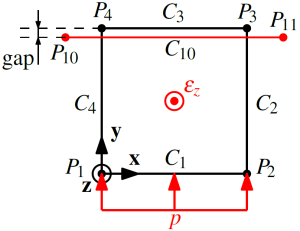
The test case in the following figure is identical to what was decribed previously. A square is pushed against a contact tool (frictionless) with a pressure $p$, its lateral movement is blocked and its out-of-plane thickness increases (as a function of time).

The gap can be computed in various ways, numerically, analytically and semi-analytically/numerically. This is what is done in three different extractors to test the good implementation of the previous feature:

• numericalGap: the numerical computation simply consists in extracting the gaps in the Metafor computation and choosing the one at $P_{4}$.
• analyticalGap: the analytical computation provides the value of the gap via the following formula: $\text{gap} = p/k_{n}$, where $k_{n}$ is the normal penalty coefficient.
• semiNumAnalyGap: Thirdly, the semi-analytical/numerical computation consists in dividing the nodal contact force along $\mathbf{y}$, $f_{y}$, at $P_{4}$ by the nodal area $l_{x}l_{z}/n_{x}$ (where $l_{z} = \epsilon_{z}$, since the initial out-of-plane thickness is 1, and where $n_{x}$ is the number of elements along $\mathbf{x}$) and the normal penalty $k_{n}$: $\text{gap} = f_{y}/( k_{n}l_{z}l_{x}/(2n_{x}) )$

In all three cases, the gap should be the same (besides errors due to finite precision computation).

• The property NBR_CONTACT_INTERACTION was replaced by NUM_CONTACT_INTERACTION to make sure that the specific number of a contact interaction is provided and not the total number;
• The address of clifton was replaced by the address of blueberry in stats.py.

[a] apps/gps/contThickEvol.py

— Dominik Boemer 2018/07/17 19:00