Dans le cadre du projet HPC4WE, nous avons développé un cas-test de fluotournage en formalisme Arbitraire Lagrangien Eulérien (ALE). La simulation numérique du procédé de fluotournage est un cas relevant et de grande taille pour évaluer les performances du parallélisme en formalisme ALE. Elle est particulièrement demandeuse de ressources CPU puisque ce procédé nécessite un grand nombre de tours de rotation et donc un grand nombre de pas de temps. Nos partenaires du projet montrent un vif intérêt à la simulation numérique de ce procédé de mise à forme.

Ce cas-test de fluotournage est aussi surtout une excellente opportunité pour mettre en avant les méthodologies de modélisation développées dans METAFOR :

• le formalisme ALE permet une réduction drastique de la taille du modèle : la zone de raffinement dans la direction axiale est limitée uniquement au voisinage proche des différentes molettes pour avoir une modélisation précise des conditions de contact et de la mise à forme (voir Figure 2 ci-dessous).
• l’algorithme d’intégration temporelle implicite a l’avantage d’être inconditionnellement stable, ce qui nous permet de faire un plus petit nombre de grands incréments temporels.
• le parallélisme de nos algorithmes les plus consommateurs en ressources CPU permet une réduction drastique des temps de calcul.

La combinaison de ces trois méthodologies nous permet de limiter la taille du modèle et, surtout, de rendre accessible la simulation d’applications industrielles comme le procédé de fluotournage pour de très longs tubes.

Les jeux de données de notre modèle numérique développé en formalisme ALE s’appuient sur ceux existants du modèle Lagrangien.

Dans la simulation Lagrangienne classique du procédé, un maillage fin est requis dans la direction axiale pour avoir de bonnes conditions de contact (voir Figure 1). Le coût CPU estimé pour la simulation représentée sur la Figure 1 est de l’ordre de 10 jours avec une seule couche d’éléments finis dans l’épaisseur du tube (56400 éléments finis).

Bien évidemment, les coûts CPU deviennent inaccessibles à mesure que le nombre de couches d’éléments finis augmente puisque la taille du modèle croît très rapidement.

Figure 1 : Simulation Lagrangienne du procédé de fluotournage.

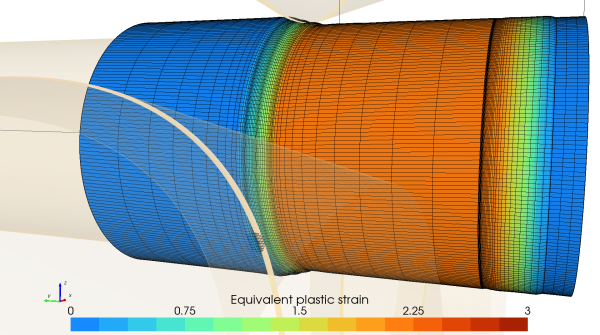
En revanche, dans la simulation ALE du procédé, un maillage fin est requis dans la direction axiale, uniquement en face des molettes mobiles (voir Figure 2). Cela nous amène à des coûts CPU qui restent acceptables dans le cas d’un nombre de couches d’éléments finis supérieur à un puisque la taille du modèle ne croît pas rapidement.

Le modèle illustré sur la Figure ci-dessous comprend 21360 éléments finis pour une seule couche d’élément dans l’épaisseur du tube. Le coût CPU est de l’ordre de 3 jours.

Figure 2 : Simulation ALE du procédé de fluotournage.

La modélisation ALE du fluotournage a nécessité le développement d’un algorithme spécifique de repositionnement des nœuds. L’algorithme implémenté est un remaillage par courbe spline qui repose sur le mailleur HybridDensityMesher1D (documenté ici).

La particularité du mailleur HybridDensityMesher1D est que celui-ci nous permet de mailler une entité géométrique 1D en choisissant le nombre $n$ de mailles (qui est constant dans le cas précis qui nous occupe) ainsi que la distribution des points. Avec ce mailleur, la distribution des points peut se faire par des points attracteurs dont il faut spécifier la coordonnée réduite, l’intensité et le poids.

L’algorithme implémenté consiste à remailler une spline, c’est-à-dire à évaluer la spline en $n-1$ coordonnées réduites qu’il faut déterminer. Pour ce faire, il nous faut alimenter le mailleur HybridDensityMesher1D avec les nouvelles coordonnées réduites des $p$ points attracteurs. Dans l’application qui nous occupe, il suffit de calculer l’intersection entre la spline et le plan à coordonnée cartésienne $Y$ égale à une constante qui contient un point géométrique choisi du congé de la molette.

• Des cas-tests 2D et 3D du fluotournage en formalisme ALE sont ajoutés (1 molette ou 3 molettes).
• Seul un cas-test 2D en formalisme ALE est exécuté dans la batterie.
• Correction dans l’en-tête des fichiers de fluotournage ($Id$).

A : oo_meta/mtALE/SplineCurveHybridDensityReZoner.h/.cpp

A : oo_nda/fluotournage/battery/tubeALE2D3M.py
A : oo_nda/fluotournage/tests/tubeALE2D1M.py
A : oo_nda/fluotournage/tests/tubeALE2D3M.py
A : oo_nda/fluotournage/tests/tubeALE3D3M.py
A : oo_nda/fluotournage/tools/fluoTournageALE2D.py
A : oo_nda/fluotournage/tools/fluoTournageALE3D.py
A : oo_nda/fluotournage/tools/fluoTournageToolsALE.py

— Yannick Crutzen 2018/01/30