Dans le cadre du projet HPC4WE, j'ai introduit le parallélisme dans des algorithmes de repositionnement des nœuds du pas Eulérien.

Les algorithmes de remaillage par courbe spline comprennent deux étapes successives :

1. Une boucle sur les nœuds intérieurs des courbes pour le calcul des nouvelles positions. Ces nouvelles positions sont stockées temporairement dans un vecteur.
2. Une boucle sur les nœuds intérieurs pour écrire les nouveaux déplacements dans la base de données.

Il est important de réaliser cette opération de remaillage en deux temps, c’est-à-dire en deux boucles indépendantes, pour ne pas modifier la géométrie de la courbe spline durant l’évaluation de la position.

Les itérations de la première boucle étant indépendantes, j’ai rendu cette première boucle parallèle sans aucun problème.

Dans la modélisation ALE du profilage, les nœuds appartenant aux faces supérieure et inférieure de la bande sont repositionnés en les projetant sur une surface spline, qui est reconstruite à partir de la configuration Lagrangienne courante du maillage. Cette technique de reconstruction de surface spline est couplée à une méthode de lissage Laplacien pondéré. Cette dernière consiste à écrire en chacun des nœuds l’équation suivante : \begin{equation} \boldsymbol{x}_0 = \frac{1}{\sum \omega_i} \sum_{i=1}^n \omega_i \boldsymbol{x}_i \label{eq:Laplacian2DReZoner} \end{equation} Cette équation lie la position d’un nœud $\boldsymbol{x}_i$ à celle de ses $n$ proches voisins. Les poids $\omega_i$ sont calculés sur le maillage initial pour conserver un maillage similaire (conservation des proportions des différentes mailles d’un maillage structuré localement raffiné) lors du processus de lissage. Dans METAFOR, la résolution du système d’équations résultant s’appuie sur une méthode itérative de Gauss-Seidel. Cette dernière consiste à résoudre successivement chacune des équations du système en utilisant continuellement les positions les plus à jour dont on dispose.

Tout d’abord, il faut souligner que les appels concurrents des opérateurs de projection sont permis depuis les travaux de Gaëtan. Ce commit se focalise donc à implémenter le parallélisme dans la méthode de lissage Laplacien.

L’option retenue consiste à mettre en place une méthode de Jacobi dans le but de s’affranchir des relations de dépendance entre les itérations de la boucle. Autrement dit, la nouvelle position du nœud est calculée à partir de la position de ses $n$ proches voisins non actualisée par le lissage. De cette manière, les relations de dépendance entre les positions des nœuds, soit des itérations de la boucle, sont éliminées. Pour ce faire, contrairement à la méthode de Gauss-Seidel, les nouvelles positions calculées sont tout d'abord stockées temporairement dans un vecteur. Ensuite, une fois la boucle parallèle terminée, les nouveaux déplacements sont écrits dans la base de données avec une boucle série.

Cette nouvelle méthode de résolution de Jacobi est implémentée dans la classe IterativeReZoner2D. De toute évidence, toutes les méthodes de repositionnement qui dérivent de la classe IterativeReZoner2D héritent de cette nouvelle méthode de résolution. Néanmoins, il faut noter que, à ce stade, je n'ai testé cette méthode de résolution de Jacobi qu’avec la seule méthode de lissage Laplacien pondéré pour le traitement des surfaces, tel qu’utilisée dans nos modèles ALE de profilage.

Le choix de la méthode de résolution se fait par la méthode d’interfaçage suivante : useJacobi(bool f). Le choix par défaut est la méthode de Gauss-Seidel (f=false) et la boucle d’itérations reste dans ce cas purement série. En revanche, dans le cas précis de la méthode de Jacobi, la boucle d’itérations est toujours exécutée de manière concurrente.

Par ailleurs, il est à noter que des attributs membres de la classe IterativeReZoner2D (mtMath::Vect3 workingPlane; mtMath::Vect3 tgX; mtMath::Vect3 tgY; mtMath::Vect3 origin; std::vector<mtGeo::Curve *> ptEdges; std::vector<mtGeo::Side *> ptSides;) sont passés en argument des méthodes de classe puisque ce sont des données non-partagées entre les différents threads dans le cas de la méthode de Jacobi.

Enfin, j’ai ajouté un verrou (tbb::spin_mutex) qui est indispensable dans le calcul des résidus de la méthode de repositionnement dans les cas où nous voulons les calculer avec la méthode de Jacobi (verbose ou saveFile).

Les performances en parallélisme ont été évaluées pour une simulation ALE de profilage.

Figure 1: Speedup.

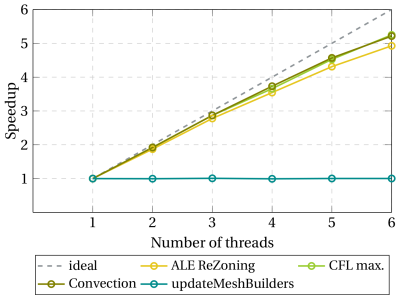
Figure 2: Speedup dans le pas Eulérien.

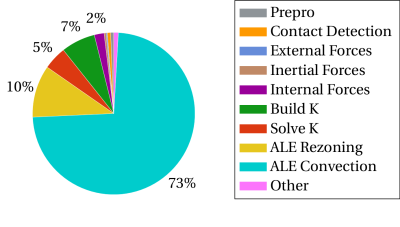
Figure 3: Répartition du temps d'horloge (1 thread).

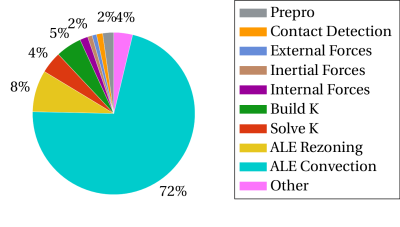
Figure 4: Répartition du temps d'horloge (6 threads).

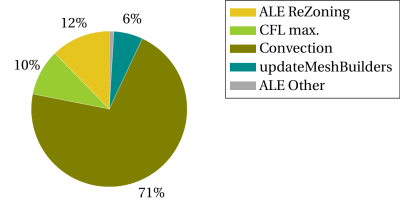
Figure 5: Répartition du temps d'horloge dans le pas Eulérien (1 thread).

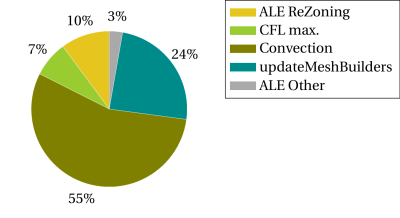
Figure 6: Répartition du temps d'horloge dans le pas Eulérien (6 threads).

Les remarques suivantes peuvent être formulées :

• L'efficacité parallèle de nos algorithmes de repositionnement des nœuds se révèle, en somme, convaincante puisque nous atteignons un speedup d'environ 5 avec 6 threads.
• L'efficacité parallèle de la convection reste limitée par la mise à jour série du maillage volume fini (updateMeshBuilders). En effet, le temps passé dans les multiples mises à jour du maillage auxiliaire (maillage volumes finis) occupe une place de plus en plus significative dans la convection ALE à mesure que le nombre de threads imposés augmente. Elle atteint 24% du temps du pas Eulérien avec 6 threads imposés. Ces routines sont exécutées par un seul thread et sont une raison majeure de l'efficacité parallèle limitée de la partie globale de la convection du pas Eulérien.

Dans les petits cas-tests de collage ALE de la batterie (apps.sticking), la méthode de Gauss-Seidel est remplacée par la nouvelle méthode de Jacobi.

— Yannick Crutzen 2018/01/17