Table of Contents
Commit 2016-01-05
Elément de collage par ressort
Contexte et motivations
Dans nos modèles numériques du disque aubagé (blisk), nous avons jusqu'à présent recours à des éléments de contact avec un matériau collant puisque les maillages des pieds d'aubes et du tambour sont incompatibles à leur interface. Avec ces éléments de collage par contact, nous rencontrons les problèmes et faiblesses suivants :
- En dépouillant nos premiers résultats pour un chargement centrifuge du blisk, le déplacement de points caractéristiques en tête et pied d'aube a retenu notre attention (voir Figure 1 et Figure 2). Nous avons observé, dès le terme du premier pas d'intégration, un déplacement radial négatif non négligeable (qui atteint sa valeur maximale (-0.45 mm) sur le bord d'attaque au pied d'aube). Ce déplacement a une origine purement numérique : notre traitement numérique du collage du pied d'aube sur le tambour referme le jeu radial existant initialement entre ceux-ci. Vu la projection des noeuds esclave de l'aube sur le tambour, des forces de contact s'exercent sur le pied d'aube et le tambour de manière à refermer ce jeu initial et génèrent, par la même occasion, une surestimation de concentration de contraintes sur le pied d'aube. Cet artéfact numérique entraîne surtout, à son tour, une maîtrise particulièrement délicate du jeu radial entre la tête d'aube et le carter, qui est lui-même consommé par déformation centrifuge du blisk. Or, une maîtrise fine de ce jeu radial est précisément l'une des pièces maîtresses de notre modélisation du contact aube/carter dans des conditions spécifiées (une profondeur d'incursion donnée de la tête d'aube dans la cartouche abradable quelque soit le régime de rotation considéré).
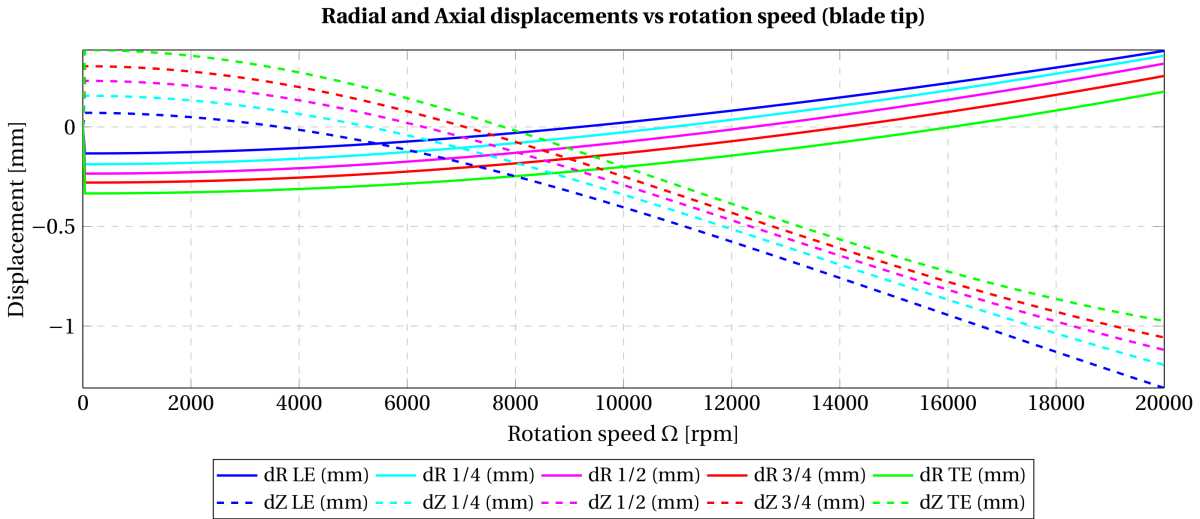 Figure 1 – Evolution des déplacements radial et axial de points caractéristiques en tête d'aube en fonction de la vitesse de rotation – Chargement centrifuge quasi-statique du modèle de disque aubagé avec une technique de collage par contact bilatéral.
Figure 1 – Evolution des déplacements radial et axial de points caractéristiques en tête d'aube en fonction de la vitesse de rotation – Chargement centrifuge quasi-statique du modèle de disque aubagé avec une technique de collage par contact bilatéral.
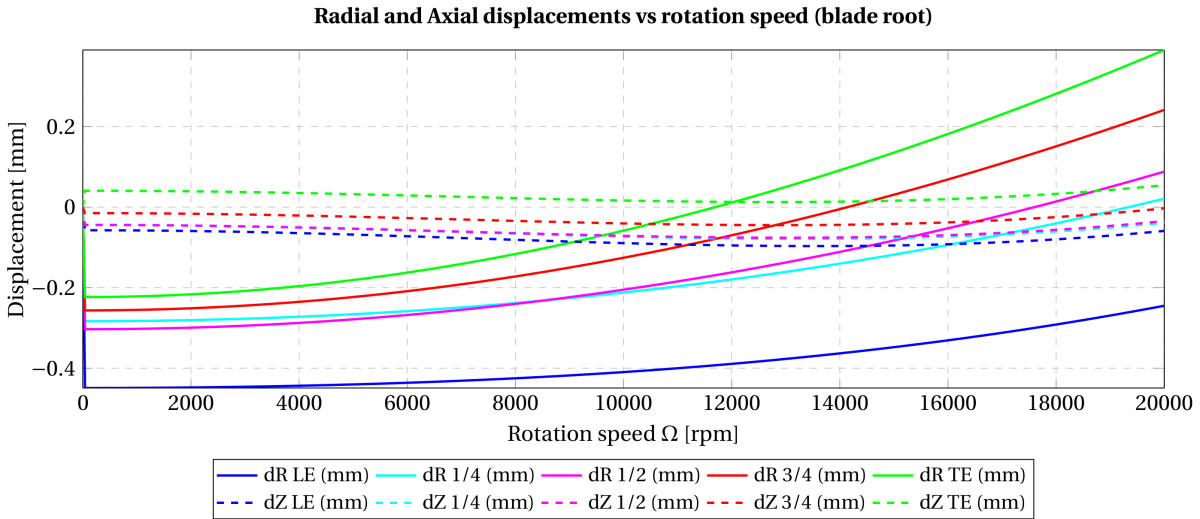 Figure 2 – Evolution des déplacements radial et axial de points caractéristiques au pied d'aube en fonction de la vitesse de rotation – Chargement centrifuge quasi-statique du modèle de disque aubagé avec une technique de collage par contact bilatéral.
Figure 2 – Evolution des déplacements radial et axial de points caractéristiques au pied d'aube en fonction de la vitesse de rotation – Chargement centrifuge quasi-statique du modèle de disque aubagé avec une technique de collage par contact bilatéral.
- Nos modèles numériques du disque aubagé sont très demandeurs de ressources CPU si nous voulons simuler un grand nombre de tours. L'algorithme de contact utilisé pour le collage est réputé extrêmement coûteux en termes de temps CPU. Les raisons suivantes peuvent être avancées :
- La détection du contact nécessite, pour un contact de type défo-défo comme dans le cas qui nous occupe ici, une recherche extrêmement coûteuse de projections géométriques. En comparaison d'un contact rigide-défo, la perte de l'unicité de la projection et de la continuité de la normale de l'entité maître induisent un calcul très onéreux de toutes les projections.
- Pour l'élément de contact défo-défo, seule la matrice de raideur tangente numérique est disponible à ce jour dans Metafor. L'évaluation de la matrice de raideur tangente numérique est elle-même responsable d'un coût de calcul supérieur, en comparaison d'une matrice de raideur tangente analytique.
- L'évaluation de la matrice de raideur tangente numérique nous prive de son assemblage en parallèle, ce qui nous empêche aussi de tirer considérablement nos coûts de calcul vers le bas.
- La valeur du paramètre numérique de pénalité normale de nos éléments de collage par contact est l'objet d'un compromis qui peut être difficile à trouver, voire précaire. Si sa valeur est basse, il nous faut tolérer une grande inter-pénétration des mailles à coller, ainsi qu'une participation sur les premiers modes propres et fréquences propres associées. Pour l'application qui nous occupe (le but ultime étant la reproduction d'un phénomène de divergence du premier mode de torsion (1T) d'aube au voisinage d'un régime de rotation critique avec une interaction aube/carter abradable), ces deux aspects ne tiennent assurément pas du détail. A contrario, si la valeur du paramètre de pénalité normale est choisie trop élevée, le conditionnement de la matrice de raideur tangente peut se dégrader et des problèmes de convergence parfois fatals peuvent être rencontrés.
En définitive, des progrès sur notre stratégie numérique de collage actuelle sont souhaités et même indispensables pour atteindre nos objectifs en matière de simulations avec le disque aubagé.
Revue des techniques numériques de collage envisagées
Pour contrecarrer les problèmes précités avec la technique de collage par contact bilatéral, nous proposons le plan d’actions suivant :
- Développement d'un élément de collage basé sur un modèle de ressort. Il s'agit d'une première étape indispensable pour éliminer le phénomène indésirable observé sur le déplacement des noeuds des éléments de collage par contact en présence d'un jeu initial entre les mailles. Toutefois, cette approche de conception relativement simple est sans réelle finalité pour l'analyse fréquentielle. Il nous faut en effet, comme pour les éléments de collage par contact, espérer une convergence des premières fréquences propres d'intérêt pour des grandes valeurs du paramètre de raideur de l'élément de collage.
- Développement d'un élément de collage avec élimination de degrés de liberté. De cette manière, nous pourrions nous libérer de la raideur introduite précédemment avec le modèle de ressort. Cette méthode s'appuierait en partie sur les développements mis en oeuvre précédemment pour la méthode de collage par modèle de ressort, notamment en ce qui concerne la recherche de l'élément maître.
- Développement d'un élément de collage avec multiplicateur de Lagrange. Malgré que les multiplicateurs de Lagrange ne soient pas la panacée dans notre service, nous pouvons espérer qu'ils soient adaptés s'ils restent cantonnés au cas particulier du collage.
Description d'une nouvelle méthode numérique de collage basée sur une modélisation de type ressort
Initialisation/construction de l'élément de collage
Recherche de l'élément maître
En premier lieu, avant toute intégration temporelle (plus précisément lors du remplissage du locel de l'élément de collage), nous recherchons l'élément maître associé au noeud esclave. Pour ce faire, nous recherchons tout d'abord, parmi les noeuds de l'entité maître, le noeud géométriquement le plus proche du noeud esclave. Ensuite, sur base de ce noeud le plus proche, nous remontons à ses différents éléments parents et nous sélectionnons l'élément maître de la manière suivante :
- Si le noeud esclave se trouve à l'intérieur de l'un des éléments parents, l'élément maître est cet élément parent.
- Si le noeud esclave ne se trouve à l'intérieur d'aucun élément parent, nous choisissons, comme élément maître, l'élément pour lequel les coordonnées réduites du noeud esclave sont les plus proches de l'une des frontières de l'élément (à condition que le noeud esclave soit à une distance inférieure à une tolérance définie par l'utilisateur). La valeur par défaut de cette tolérance géométrique extérieure est 0.3.
- Si le noeud esclave ne se trouve à l'intérieur d'aucun élément parent et si sa distance par rapport à l'élément excède la tolérance géométrique extérieure, alors une erreur fatale est générée.
Cette technique de recherche est largement reprise de la méthode findElemIp(mtMath::Vect3 &pos) implémentée dans la classe GeoPointValueExtractor.
Il est à noter que nous considérons pour l'heure, comme élément maître, tout élément fini incident au noeud trouvé, en ce compris les éléments qui n'appartiennent pas à l'entité géométrique maître.
Soulignons que, en comparaison des éléments de collage par contact, nous nous affranchissons de nos opérateurs de projection à chaque début d'itération, ce qui confère un avantage technique considérable en termes de coût de calcul.
Calcul des coordonnées réduites du noeud esclave et de la valeur des fonctions de forme
Une fois l'élément maître identifié, nous évaluons successivement sur la configuration initiale uniquement :
- les coordonnées réduites du noeud esclave $(\xi_0, \eta_0, \zeta_0)$;
- la valeur des $n$ fonctions de forme de l'élément maître évaluées aux coordonnées réduites du noeud esclave $N_i (\xi_0, \eta_0, \zeta_0)$.
Vecteur des coordonnées généralisées
Le vecteur des coordonnées généralisées de l'élément de collage est : \begin{equation} \boldsymbol{q}_e = \begin{bmatrix} \boldsymbol{X}_{\text{slave}} \\ \boldsymbol{X}_1 \\ \boldsymbol{X}_2 \\ \vdots \\ \boldsymbol{X}_n \end{bmatrix} \label{eq:q_e} \end{equation} où $\boldsymbol{X}_{\text{slave}}$ est le vecteur des coordonnées du noeud esclave et $\boldsymbol{X}_1$, $\boldsymbol{X}_2$, …, $\boldsymbol{X}_n$ sont les vecteurs des coordonnées des $n$ noeuds de l'élément maître.
Calcul du vecteur des forces internes
Le vecteur élémentaire des forces internes s'écrit : \begin{equation} \boldsymbol{F}_e^{\text{int}}(\boldsymbol{q}_e) = \begin{bmatrix} \boldsymbol{F}_{\text{spring}} \\ -N_1 (\xi_0, \eta_0, \zeta_0) \boldsymbol{F}_{\text{spring}} \\ -N_2 (\xi_0, \eta_0, \zeta_0) \boldsymbol{F}_{\text{spring}} \\ \vdots \\ -N_n (\xi_0, \eta_0, \zeta_0) \boldsymbol{F}_{\text{spring}} \end{bmatrix} \label{eq:Fint} \end{equation} où $\boldsymbol{F}_{\text{spring}}$ est la force de rappel de ressort et $N_1 (\xi_0, \eta_0, \zeta_0)$, $N_2 (\xi_0, \eta_0, \zeta_0)$, …, $N_n (\xi_0, \eta_0, \zeta_0)$ sont les $n$ fonctions de forme de l'élément maître évaluées aux coordonnées réduites du noeud du esclave à la configuration initiale.
La force de rappel de ressort s'écrit : \begin{equation} \boldsymbol{F}_{\text{spring}} = f \boldsymbol{e} \label{eq:Fspring} \end{equation} où $f$ et $\boldsymbol{e}$ sont respectivement l'amplitude et le vecteur directeur de norme unitaire de la force de rappel du ressort. En toute généralité, l'amplitude de la force $f$ s'écrit : \begin{equation} f = k \left( \left\| \boldsymbol{X}_{\text{slave}} - \boldsymbol{X}_{\text{ref}} \right\| - l_0 \right) \label{eq:force} \end{equation} où $k$, $\boldsymbol{X}_{\text{ref}}$ et $l_0$ sont respectivement la raideur de ressort, les coordonnées d'un noeud de référence et la longueur de repos.
Connaissant les coordonnées nodales de l’élément maître à la configuration courante et la valeur des fonctions de forme de l'élément maître évaluées en les coordonnées réduites de la configuration initiale, nous pouvons calculer les coordonnées du noeud de référence selon la relation ci-dessous. Notons que, dans sa configuration initiale, les 2 noeuds formant le ressort sont géométriquement confondus, sa force interne est nulle. Il est également à noter que le noeud de référence est “fictif” : les forces internes sont distribuées sur les noeuds de l'élément maître via une pondération des fonctions de forme. En l'occurrence, il n'appartient pas à la base de données nodales.
\begin{equation} \boldsymbol{X}_{\text{ref}} = \sum_i^n N_i (\xi_0, \eta_0, \zeta_0) \boldsymbol{X}_{\text{i}} \label{eq:Xref} \end{equation}
Le vecteur directeur de la force $\boldsymbol{e}$ est : \begin{equation} \boldsymbol{e} = \frac{\boldsymbol{X}_{\text{ref}} - \boldsymbol{X}_{\text{slave}}}{\left\| \boldsymbol{X}_{\text{ref}} - \boldsymbol{X}_{\text{slave}} \right\|} \label{eq:e} \end{equation}
Dans le cas particulier de l'élément de collage, il est important de noter que la longueur de repos $l_0$ est nulle. Dès lors, l'expression de la force de rappel de ressort se simplifie de la manière suivante. \begin{equation} \boldsymbol{F}_{\text{spring}} = \text{f} \boldsymbol{e} = k \left( \boldsymbol{X}_{\text{ref}} - \boldsymbol{X}_{\text{slave}} \right) \label{eq:Fspring1} \end{equation}
Point notable : dans le cas d'un jeu entre le noeud à coller et l'élément maître, certaines fonctions de forme sont bien évidemment de valeur négative. D'après nos premières expériences (cas-tests sur des mono-éléments et sur le modèle de blisk), ces valeurs négatives sont relativement marginales et ne posent pas de problèmes particuliers.
Dérivation analytique de la matrice de raideur tangente
La matrice de raideur tangente élémentaire est calculée par simple dérivation du vecteur élémentaire des forces internes (sous sa forme simplifiée) par rapport à chacune des coordonnées généralisées de l'élément de collage. Nous avons successivement :
\begin{equation} \frac{\partial \boldsymbol{F}_{\text{spring}}}{\partial \boldsymbol{X}_{\text{slave}}} = - k \boldsymbol{I} = \boldsymbol{K}_{11} \label{eq:dfdXslave} \end{equation}
\begin{equation} \frac{\partial \boldsymbol{F}_{\text{spring}}}{\partial \boldsymbol{X}_{i}} = k N_i \boldsymbol{I} = - N_i \boldsymbol{K}_{11} \label{eq:dfdXi} \end{equation}
\begin{equation} \frac{- N_i \partial \boldsymbol{F}_{\text{spring}}}{\partial \boldsymbol{X}_{\text{slave}}} = - N_i \frac{\partial \boldsymbol{F}_{\text{spring}}}{\partial \boldsymbol{X}_{\text{slave}}} = -N_i \boldsymbol{K}_{11} \label{eq:dNifdXslave} \end{equation}
\begin{equation} \frac{- N_i \partial \boldsymbol{F}_{\text{spring}}}{\partial \boldsymbol{X}_{j}} = - N_i \frac{\partial \boldsymbol{F}_{\text{spring}}}{\partial \boldsymbol{X}_{j}} = N_i N_j \boldsymbol{K}_{11} \label{eq:dNifdXj} \end{equation}
Finalement, l'expression analytique de la matrice de raideur tangente s'écrit :
\begin{equation} \boldsymbol{K}_e^{T} = \begin{bmatrix} \boldsymbol{K}_{11} & -N_1 \boldsymbol{K}_{11} & -N_2 \boldsymbol{K}_{11} & \dots & -N_n \boldsymbol{K}_{11} \\ -N_1 \boldsymbol{K}_{11} & N_1^2 \boldsymbol{K}_{11} & N_1 N_2 \boldsymbol{K}_{11} & \dots & N_1 N_n \boldsymbol{K}_{11} \\ -N_2 \boldsymbol{K}_{11} & N_1 N_2 \boldsymbol{K}_{11} & N_2^2 \boldsymbol{K}_{11} & \dots & N_2 N_n \boldsymbol{K}_{11} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ -N_n \boldsymbol{K}_{11} & N_1 N_n \boldsymbol{K}_{11} & N_2 N_n \boldsymbol{K}_{11} & \dots & N_n^2 \boldsymbol{K}_{11} \end{bmatrix} \label{eq:KT} \end{equation}
Mentionnons également que cette dérivation analytique se limite aux seules méthodes d'intégration non conservatives.
Interaction de collage
Une classe StickingInteraction est ajoutée dans le code.
De manière analogue aux interactions de contact, nous pouvons spécifier, pour une interaction de collage, ses entités géométriques esclave et maître via les fonctions push() et setTool() respectivement.
Matériau de collage
Le matériau de collage s'appuie logiquement sur les matériaux déjà existants pour l'élément de ressort. Malgré que les matériaux de ressort soient directement empruntés, l'élément de collage ne peut nécessairement en partager toutes leurs fonctionnalités. En particulier, rappelons que nous ne considérons pour l'heure aucune contribution de l'amortissement matériau dans la matrice de raideur tangente analytique de l'élément de collage.
StickingElShcuts
De manière analogue aux éléments de mécanisme, une classe StickingElShcuts a été ajoutée.
Ses attributs sont :
- une référence vers un matériau de type ressort.
- une tolérance géométrique extérieure exprimée en termes de coordonnées réduites dans les opérations de recherche de l'élément maître. Cette tolérance géométrique peut être définie par l'utilisateur dans les propriétés de l'élément de collage au moyen du mot-clé
OUTSIDETOL. - la méthode de calcul de la matrice de raideur tangente :
STIFFMETHOD = STIFF_NUMERICou bienSTIFFMETHOD = STIFF_ANALYTIC.
Résultats de l'application des éléments de collage par ressort au modèle du disque aubagé
Avec les éléments de collage par ressort, nous observons sur notre modèle du disque aubagé que :
- L'artéfact numérique sur les déplacements radial et axial des points caractéristiques de l'aube est totalement éliminé. De même, la concentration de contraintes excessives au pied d'aube est éliminée.
- Comme dans le cas des éléments de collage par contact, nous avons convergence des premières fréquences propres si nous considérons une grande valeur de la raideur de ressort.
- Alors que les éléments de collage par ressort auguraient de meilleures performances en ressources CPU en comparaison des éléments de collage par contact (matrice de raideur tangente analytique et absence totale de détection du contact dans un contexte défo-défo), les temps de calcul connaissent une légère hausse. Pour la simulation d'un tour, dans le cas d'un seul thread, le temps de calcul passe d'environ 25 min à 30 min. Cela s'explique par un plus grand nombre d'itérations mécaniques. Le nombre de pas est identique. Toutefois, soulignons que nous simulons un problème différent (voir première observation).
Cas-tests de la batterie
De nouveaux cas-tests sont ajoutés à notre batterie dans le répertoire apps/sticking/.
Ils permettent de tester les éléments de collage par ressort dans le cas de grands déplacements ou grandes rotations imposés, avec une matrice de raideur analytique ou numérique, avec une interpénétration initial des mailles à coller ou un jeu initial entre les mailles à coller.
Perspectives
- Contribution de l'aire de collage nodale pour s'affranchir de la dépendance à la densité du maillage.
- Visualisation des éléments de collage par ressort dans la fenêtre VizWin.
- Développement de l'élément de collage avec élimination de degrés de liberté.
- Développement de l'élément de collage avec multiplicateur de Lagrange.
Divers
- Suppression d'opérations de calcul inutiles dans la méthode
interpolate(const std::vector<mtMath::Vect3> &nodalValues) constde la classeSfIntegrationPointTemplate<DIMSF>. - Suppression d'opérations de calcul inutiles dans la méthode
getGaussPointPosition(int integNo, int i, const Configuration &conf)de la classeVolumeElement_ale.
Fichiers ajoutés/supprimés
Added : oo_meta\mtElements\sticking\StickingElement.h Added : oo_meta\mtElements\sticking\StickingElement.cpp Added : oo_meta\mtElements\sticking\StickingElement.inl Added : oo_meta\mtElements\sticking\StickingElShcuts.h Added : oo_meta\mtElements\sticking\StickingElShcuts.inl Added : oo_meta\mtElements\sticking\StickingInteraction.h Added : oo_meta\mtElements\sticking\StickingInteraction.cpp
Tests ajoutés/supprimés
Added : oo_meta\apps\sticking\monos2d.py Added : oo_meta\apps\sticking\monos2dNumStiff.py Added : oo_meta\apps\sticking\monos3d.py Added : oo_meta\apps\sticking\monos3dClearance.py Added : oo_meta\apps\sticking\monos3dNumStiff.py Added : oo_meta\apps\sticking\monos3dRot.py Added : oo_meta\apps\sticking\monos3dRotClearance.py
— Yanick Crutzen 2016/01/05
