• Définition d'un système d'axe particulier dans les matériaux:
  • Un système d'axe Orthotrope est défini dans les matériaux de manière à pouvoir d'une part travailler l'anisotropie et d'autre part ressortir des contraintes dans un système d'axe local (typiquement pouvoir sortir les contraintes dans le plan d'une tôle emboutie,…)
  • Le système d'axe reste Orthotrope et suit la rotation (externe et interne) du matériau par l'accumulation des rotations de Jaumann
  • Les InternalFields suivant sont ajoutés à la sortie des courbes - visualisation des champs :
    • IF_DEV_SIG_ORTHO_XX, “Deviatoric Sigma Ortho XX”
    • IF_DEV_SIG_ORTHO_YY, “Deviatoric Sigma Ortho YY”
    • IF_DEV_SIG_ORTHO_ZZ, “Deviatoric Sigma Ortho ZZ”
    • IF_SIG_ORTHO_XX, “Sigma Ortho XX”
    • IF_SIG_ORTHO_YY, “Sigma Ortho YY”
    • IF_SIG_ORTHO_ZZ, “Sigma Ortho ZZ”
    • IF_SIG_ORTHO_XY, “Sigma Ortho XY”
    • IF_SIG_ORTHO_XZ, “Sigma Ortho XZ”
    • IF_SIG_ORTHO_YZ, “Sigma Ortho YZ”
  • L'entrée du système d'axe Ortho initial se fait via les propriétés du matériau :
    • ORTHO_AX1_X (defaut : 1.0)
    • ORTHO_AX1_Y (defaut : 0.0)
    • ORTHO_AX1_Z (defaut : 0.0)
    • ORTHO_AX2_X (defaut : 0.0)
    • ORTHO_AX2_Y (defaut : 1.0)
    • ORTHO_AX2_Z (defaut : 0.0)

Le système d'axe est reconstruit - renormé (on peut rentrer un axe (1,1,1))

• Gestion de l'objectivité:
  • L'objectivité de la dérivée des contraintes est assurée en définissant une dérivée corotationelle des contraintes (dans un système d'axe tournant avec la matière). La rotation du système d'axe peut être calculée incrémentalement par l'accumulation des tenseurs rotations déduits de la décomposition du tenseur taux de déformation :
  • Jaumann :
    • $$ F_{n->n+1} = R_{n->n+1} U_{n->n+1} $$
    • $$ \sigma_{n+1} = R^T_{n->n+1} (\sigma_{n} + H ln(U_{n->n+1})) R_{n->n+1} $$

• Green-Naghdi :
  • $$ F_{n->n+1} = R_{n->n+1} U_{n->n+1} $$
  • $$ F_{0->n+1} = R_{0->n+1} U_{0->n+1} $$
  • $$ \sigma_{n+1} = R^{T}_{0->n+1} R_{0->n} (\sigma_{n} + H ln(U_{n->n+1})) R^{T}_{0->n} R_{0->n+1} $$

• Critère de plasticité de Hill 48:
  • le critère de plasticité de VonMises s'écrit :

$$ \sqrt{\frac{3}{2}s_{ij}s_{ij}} - \sigma_{vm} = 0 $$

• le critère de plasticité de Hill48 s'écrit :

$$\sqrt{\frac{1}{2}} \sqrt{F (s_{22}-s_{33})^2 + G (s_{33}-s_{11})^2 + H (s_{11}-s_{22})^2 + 2 (L s_{13}^2 + M s_{23}^2 + N s_{12}^2) }- \sigma_{vm} = 0 $$

• Le critère de Hill nécessite donc de définir les 6 paramètres Hill48_F, Hill48_G, Hill48_H, Hill48_L, Hill48_M, Hill48_N et le système d'axes orthotropes dans lequel ils ont été mesurés.
• Génération d'un classe mère et d'une chaine de dérivation PlasticCriterion définissant le critère de plasticité et toutes les fonctions spécifiques associées. La classe dérive de MaterialLaws et par défaut, le critère de VonMises est défini.
• Modification du matériau élasto-visco-plastique à écrouissage isotrope (evpIsoHHypoMaterial) pour l'utilisation de la classe Plastic criterion. La classe a aussi été définie et en partie utilisée dans les autres matériaux (ça demande encore des développements).
• Pour l'instant, le calcul du critère de Hill se fait à l'aide de vecteur Normaux à la surface de plasticité non normé. Il en résulte la possibilité de retrouver une relation directe entre les contraintes, le prédicteur élastique et Gamma (n'ayant plus tout à fait la même signification).
• Suppression d'un bon nombre d'appel à la fonction .J2() (souvent abusivement utilisée) au profit du getCriterion.getF() ou de .getNorm() selon l'usage.

• EvpIsoHHypoMaterial :
  • Une estimation du gammaMax est calculée pour l'écrouissage isotrope (Faudra vérifier dans le cas où on aurait un adoucissement + très important).

• HypoMateShcuts (et dérivées) :
  • Prise en compte de la dérivation pour la définition des Shcuts, des fonctions checkPrmat et updatePrmat :
    • DEFGETSETMACRO_C(double, e, E);
    • DEFGETSETMACRO_C(double, nu, Nu);
    • DEFGETSETMACRO_C(double, g, G);
    • DEFGETSETMACRO_C(double, g2, G2);
    • DEFGETSETMACRO_C(double, k, K);
    • DEFGETSETMACRO_C(double, k3, K3);
    • DEFGETSETMACRO_C(double, rho, Rho);
    • DEFGETSETMACRO_C(bool, loiRho, LoiRho);
    • DEFGETSETMACRO_C(bool, isJaumannOrGreenNaghdi, IsJaumannOrGreenNaghdi); True = Jaumann - False = Green-Naghdi
    • DEFGETSETMACRO_C(OEMTK::Matr3, orthoAxes, OrthoAxes);
  • To Be Continued (gestion unifiée de la variation des paramètres matériaux !!!)

• MaterialLaws :
  • Modification de l'interface vers la viscosité plastique (on passe $ \Delta evpl $ à la place de gamma )
  • Modification des fonctions ElasticPredictorKh. La rotation faisant dorénavant partie du critère de plasticité.

• oeMath :
  • Ajout des fonctions :
    • double SymMatr2::getNorm() const
    • double SymMatr3::getNorm() const $ norm = \sqrt{X_{ij} X_{ij}} $
    • void SymMatr3::setToQtSymQ(const Matr3 & Q)
    • void SymMatr3::setToQtSymQ(const Matr3 & Q)

• FourthOrderTensor3D :
  • Ajout des fonctions :
    • void rotate(const OEMTK::Matr3 &R);
    • virtual void write(std::ostream &out, const Indentor &indent=Indentor(), const WOpt::flags &opts=WOpt::all)const ;
    • friend MTMATH_API std::ostream &operator«(std::ostream &out, const FourthOrderTensor3D &obj);

• VectorToScalarOperator :
  • Ajout d'un opérateur de norme (à l'ordre 2)

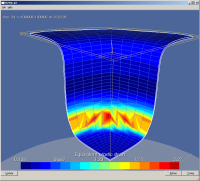
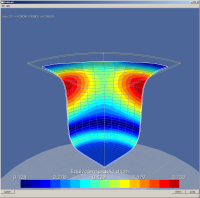
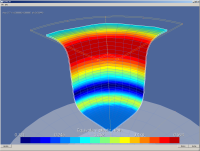
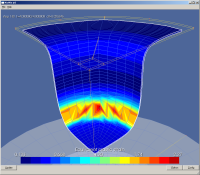
Il s'agit de l'emboutissage d'un godet cylindrique d'après le benchmark Numisheet (Attention, ce n'est pas le test exacte, n'ayant pas (encore) retrouvé la doc du Bench) (apps.qs.godetNumisheetHill48).

Les performance informatique sont étonnement peu pénalisantes : (sachant que la plasticité étant différente l'évolution du process est différent !)

• Von Mises :

      [TSC-STP]                         Number of steps : 188
      [TSC-ITE]              Number of mech. iterations : 499
      [TSC-CPU]                                CPU Time : 184.641
      [TSC-MEM]                        Peak Memory [Kb] : 84176

• Hill48 :

      [TSC-STP]                         Number of steps : 228
      [TSC-ITE]              Number of mech. iterations : 620
      [TSC-CPU]                                CPU Time : 215.031
      [TSC-MEM]                        Peak Memory [Kb] : 85020

Hill48 Isotropie Planaire :

      [TSC-STP]                         Number of steps : 217
      [TSC-ITE]              Number of mech. iterations : 579
      [TSC-CPU]                                CPU Time : 205.594
      [TSC-MEM]                        Peak Memory [Kb] : 85224 

Hill48 Isotrope (Paramètres Hill pour récuperer VonMises):

      [TSC-STP]                         Number of steps : 180
      [TSC-ITE]              Number of mech. iterations : 470
      [TSC-CPU]                                CPU Time : 167.406
      [TSC-MEM]                        Peak Memory [Kb] : 84412

Attention : Nouveau répertoire (cvs update -d ou cliquer le bouton “ajouter ) !!!

A mtMaterialLaws/PlasticCriteria
A mtMaterialLaws/PlasticCriteria/PlasticCriterion.h / cpp
A mtMaterialLaws/PlasticCriteria/PlasticCriterionShcuts.h / inl
A mtMaterialLaws/PlasticCriteria/VonMisesPlasticCriterion.h / cpp
A mtMaterialLaws/PlasticCriteria/VonMisesPlasticCriterionShcuts.h / inl
A mtMaterialLaws/PlasticCriteria/Hill48PlasticCriterion.h / cpp
A mtMaterialLaws/PlasticCriteria/Hill48PlasticCriterionShcuts.h / inl

Nouveaux Tests :

apps\monosMeca\tracRotHill48Num.py
apps\monosMeca\tracRotHill48Mat.py
apps\monosMeca\tracRotHill48Axes.py
apps\monosMeca\tracRotHill48Ana.py

apps\qs\godetNumisheetVonMises2dAxi.py 
apps\qs\godetNumisheetVonMises.py 
apps\qs\godetNumisheetHill48Isotrope2dAxi.py 
apps\qs\godetNumisheetHill48Isotrope.py 
apps\qs\godetNumisheetHill48IsoPlan2dAxi.py 
apps\qs\godetNumisheetHill48IsoPlan.py 
apps\qs\godetNumisheetHill48.py 

apps\monosMaterials\evpIsoH3dTracRotHill48Iso.py
apps\monosMaterials\evpIsoH3dTracRotHill48.py 
apps\monosMaterials\evpIsoH3dCisJaumannGreenNaghdi.py 
apps\monosMaterials\evpIsoH2dEpeTracRotHill48Iso.py 
apps\monosMaterials\apps\monosMaterials\evpIsoH2dEpeTracRotHill48.py 
apps\monosMaterials\evpIsoH2dEpeCisJaumannGreenNaghdi.py 
apps\monosMaterials\evpCinH3dCisJaumannGreenNaghdi.py 
apps\monosMaterials\evpCinH2dEpeCisJaumannGreenNaghdi.py 
apps\monosMaterials\elast3dCisJaumannGreenNaghdi.py 
apps\monosMaterials\elast2dEpeTracRotOrthoJaumann.py 
apps\monosMaterials\elast2dEpeTracRotOrthoGreenNaghdi.py 
apps\monosMaterials\elast2dEpeCisOrtho.py 
apps\monosMaterials\elast2dEpeCisJaumannGreenNaghdi.py 

— Luc PAPELEUX 2006/10/18 09:48