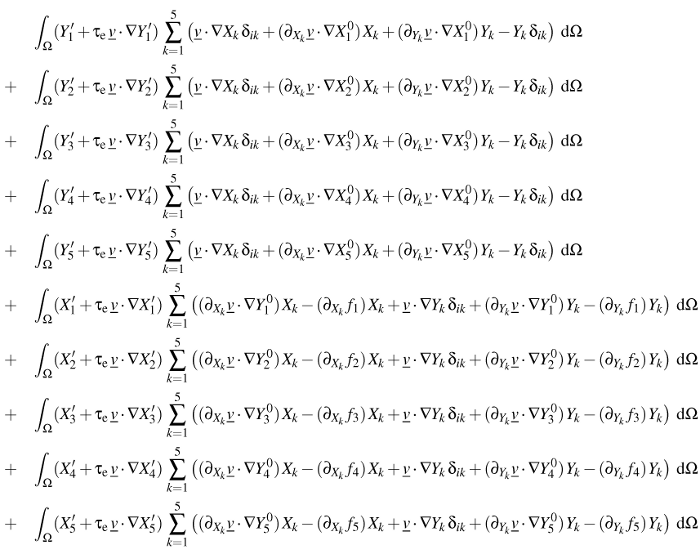Metafor

Nonlinear normal modes (NNMs) are an extension of linear normal modes to nonlinear systems. This is one of the research topics of the Space Structures & Systems Lab. (Prof. Kerschen). Actually, I knew nothing on the subject until Ludovic Renson told me about it and about the nonlinear equations he wanted to solve with finite elements. The idea to be faced with an unusual set of PDEs was too much of a temptation and I decided to implement a simple case in my old code as a test.

Rigorous definitions of NNMs can be found in references [1-2]. Here, let us consider a discrete mechanical systems with $N$ degrees of freedom. A pair of state variables $u=x_k$ and $v=y_k$ is arbitrarily chosen among the displacements $x_i(t)$ and velocities $y_i(t)$, $i\in\{1,...,N\}$. The time variable can be eliminated and the state equations are rewritten as a set of 2N-2 partial differential equations, $$\begin{eqnarray*} v\, \partial_u X_i +f_k\, \partial_v X_i &=& Y_i \\ v\, \partial_u Y_i +f_k\, \partial_v Y_i &=& f_i \\ i\in\{1,...,N\},\; i&\neq& k \end{eqnarray*}$$ The unknowns are now space variables $X_i(u,v)$ and velocities $Y_i(u,v)$. The $f_i(u,v,X_j,Y_j),\; j\neq k$ are elastic and dissipative forces in the equations of motion. These equations are solved in a two-dimensional invariant manifold in phase space.

$\vec{v}=[v, f_k]$ Find $X_i\in V$ et $Y_i\in V$, $i=\{1, \ldots, 5\}$, such that $$\begin{eqnarray*} \int_\Omega (Y'_i+\tau_{\rm e}\, \vec{v}\cdot\nabla Y'_i)\, (\vec{v}\cdot\nabla X_i-Y_i) \;{\rm d}\Omega = 0\;, && \forall Y'_i \in V \;, \\ \int_\Omega (X'_i+\tau_{\rm e}\, \vec{v}\cdot\nabla X'_i)\, (\vec{v}\cdot\nabla Y_i-f_i) \;{\rm d}\Omega = 0\;, && \forall X'_i \in V \;, \end{eqnarray*}$$ with $$\begin{equation*} V = \{ f(u,v)\in H^1(\Omega):\, f(0,0)=0\} \;. \end{equation*}$$

[1] L. Renson, G. Deliége, G. Kerschen. An effective finite-element-based method for the computation of nonlinear normal modes of nonconservative systems. Meccanica, vol. 49(8), pp. 1901-1916, 2014.
[2] L. Renson. Nonlinear Modal Analysis of Conservative and Nonconservative Aerospace Structures. PhD Thesis, Université de Liège, 2014.