This is an old revision of the document!

Premier cas-test

Introduction

Je suppose dans cette section que vous avez suivi et compris le document Python in a nutshell. Vous savez donc utiliser l'interpréteur python de manière basique.

Sur cette page, je décris, ligne après ligne, les étapes qui mènent à la mise au point d'un module python (ou jeu de données) permettant d'écraser un bloc de matière par un poinçon (matrice de contact) cylindrique en état plan de déformation. Un aperçu de la déformée finale:

<html>

</html>

Vu que Metafor est en constante évolution, il est possible que la syntaxe de certaines commandes ait changé. Ce test fait partie de la batterie de tests de Metafor et évolue au fil des mises à jour. L'utilisateur peut voir la version la plus récente (correspondant à sa version) dans apps\tutorials\tutorial1.py.

Description du jeu de données

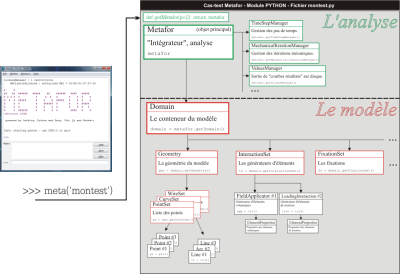
Un jeu de données Metafor est un module python définissant un objet “analyse” (nommée Metafor). Cet objet va être récupéré et manipulé par la commande meta que l'utilisateur entre en ligne de commande. L'image ci-dessous résume shématiquement l'organisation d'un module et la structure hiérarchique des différents objets qui vont intervenir dans un problème.

En résumé: un jeu de données = un (ou plusieurs) fichiers python = un objet Metafor.

Entête

Le module débute avec quelques commentaires (précédés de “#”).

# -*- coding: latin-1; -*-
# $Id$
#
# Tutorial

La ligne “coding” permet d'utiliser des caractères accentués sous python. Le “tag CVS” $Id$ (facultatif) permet de connaître la version de ce fichier.

from wrap import *
import math

Comme tous les cas-tests de Metafor, notre module importe tous les modules de Metafor dans son espace de nom. Grâce à cela, les objets de Metafor peuvent être utilisés sans être préfixés par “wrap” (wrap = wrapper littéralement “emballeur”). Il sera donc possible par exemple de parler de la classe Domain et non wrap.Domain. On importe également le module math de python (pour calculer plus loin des sinus et cosinus).

metafor = Metafor()
domain = metafor.getDomain()

On crée ensuite l'objet principal du module. Il s'agit d'un objet de type Metafor. Chaque modèle numérique traité par Metafor est articulé autour d'une analyse Metafor. Pour l'instant, il n'existe qu'un seul type d'analyse appartenant au LTAS-MN2L (d'autres sont fournies par Oofelie mais ne sont pas compilées dans l'exec de Metafor). Cette commande crée donc un objet Metafor. A partir de l'analyse metafor on peut en extraire un Domain. Le domaine est un conteneur (voir References). Il contient tous les objets nécessaires au modèle (géométrie, liste d'éléments, noeuds, fixations et autres conditions aux limites, liste de matériaux, etc).

L'analyse se charge de manipuler les données du domaine pour, par exemple, intégrer temporellement ses équations d'évolution.

La seule fonction du module nécessaire au bon fonctionnement de Metafor est la fonction getMetafor() qui doit retourner l'analyse du module (metafor). Elle sera appelée par la fonction de démarrage de Metafor (fonction meta).

def getMetafor(p={}): return metafor

Le paramètre p est un dictionnaire facultatif utilisé pour les études paramétriques.

Paramètres

Il est souvent très utile de paramétrer un modèle pour pouvoir facilement modifier des grandeurs. Il faut toujours préférer des paramètres que des valeurs écrites “en dur”. En effet, un calcul EF n'a jamais de sens s'il est effectué tout seul. Il faut toujours vérifier la solution en faisant varier les paramètres numériques. Ces paramètres peuvent être regroupés en début de fichier comme ici pour pouvoir être facilement modifiés.

Lx = 1.0  # length X
Ly = 1.0  # length Y
n1 = 10   # nb of elems on X
n2 = 10   # nb of elems on Y

On définit 4 paramètres : la longueur et la largeur du rectangle à mailler et le nombre de mailles dans les 2 directions.

Géométrie

On va ensuite créer une géométrie “utilisateur” (par opposition à la géométrie du maillage qui sera générée automatiquement lors de la création des mailles). Pour y arriver, on va récupérer une référence python vers l'objet “géométrie” (de type Geometry) du domaine que nous venons de créer:

geometry = domain.getGeometry()
geometry.setDimPlaneStrain()

La première ligne récupère la référence en faisant la demande au domaine. La seconde ligne fixe le type de géométrie. Il s'agit de l'état plan de déformation (ce pourrait être axisymétrique ou 3D – voir cmdsprelim).

TODO : Schéma en anglais par cohérence avec les notations

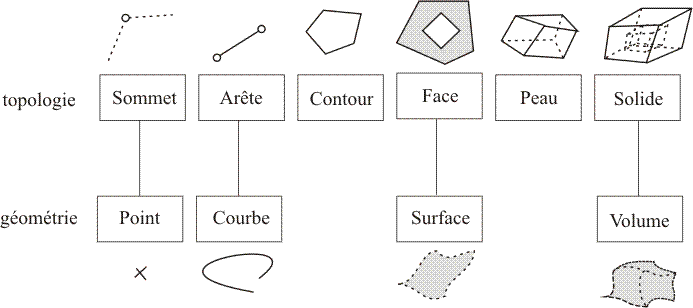
La création d'une géométrie suit toujours le même schéma (voir figure ci-dessus). Il faut savoir qu'on utilise, dans Metafor, une représentation de type B-REP (Boundary Representation) simplifiée pour laquelle chaque entité est définie comme étant un ensemble des entités de niveau inférieur. L'objet Volume, l'entité 3D de plus haut niveau, est constitué d'une ou plusieurs Skins (peaux): une skin externe (première skin) et un éventuel ensemble de trous. Une Skin est constituée d'un ensemble ordonné de Sides (faces). Une Side est un ensemble de Wires (contours): un wire externe et un éventuel ensemble de trous. On associe également une Surface à la Side. Un Wire est un ensemble ordonné de Curves (courbes) et d'objets dérivés (Line, Arc, …). Enfin, une Curve est un ensemble de Points, qui sont les entités de base de la géométrie.

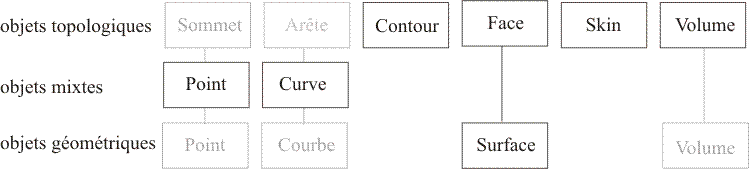
Pourquoi parle-t-on de B-REP simplifié (voir figure ci-dessous)? Parce que les concepts géométriques et topologiques sont mélangés pour les curves et les points. En effet, une curve devrait être définie comme une arête constituée de 2 sommets à laquelle on associe une géométrie.

A chaque entité géométrique est associé un ensemble (Set). Ainsi, l'objet Point se “range” dans un PointSet. Les ensembles géométriques sont contenus dans la géométrie. Pour y accéder, on utilise, comme plus haut, une fonction de type get*().

La définition des objets dans les ensembles se fait par deux techniques en fonction de la taille de l'objet à créer:

Pour les objets de petite taille qui demandent peu de paramètres pour être totalement définis (les Points mais aussi les fixations, par exemple), on utilise une fonction membre set.define().

Pour les objets qui nécessitent plus d'arguments, on crée un objet temporaire, on le remplit et on le copie dans l'ensemble (voir plus loin, lors de la définition des curves par exemple).

Ici, pour les Points, la première méthode est disponible. Le premier argument est un numéro utilisateur (strictement positif et unique pour chaque ensemble) et les 3 suivants sont les coordonnées $x, y \mbox{ et } z$. Comme on s'est placé en état plan de déformation, le plan de travail est le plan par défaut $z=0$ et seules les coordonnées $x$ et $y$ sont fournies.

pointset = geometry.getPointSet()
pointset.define(1,  0,   0)
pointset.define(2,  Lx,  0)
pointset.define(3,  Lx, Ly)
pointset.define(4,  0,  Ly)
pointset.define(5,  2*Lx,  Ly+2*Lx)
pointset.define(6,  2*Lx*math.cos(math.pi/4), 
                  Ly+2*Lx-2*Lx*math.sin(math.pi/4))
pointset.define(7, -2*Lx, Ly+2*Lx)

Nous continuons ensuite par les objets Curves:

curveset = geometry.getCurveSet()
curveset.add(Line(1, pointset(1), pointset(2)))
curveset.add(Line(2, pointset(2), pointset(3)))
curveset.add(Line(3, pointset(3), pointset(4)))
curveset.add(Line(4, pointset(4), pointset(1)))
curveset.add(Arc(5, pointset(7), pointset(6), pointset(5)))

La première ligne récupère une référence vers l'ensemble des curves, le CurveSet. Puisque les curves utilisées par Metafor peuvent être de nombreux types et parfois très complexes (Nurbs), on utilise ici la deuxième façon d'enrichir un ensemble par la création d'un objet suivie de l'ajout de cet objet dans l'ensemble. Les objets Line (segment de droite) se définissent par un numéro et les points des deux extrémités. Un Arc utilise 3 points.

Il faut remarquer également que l'arc de cercle est destiné à modéliser une matrice de contact. Son orientation a donc de l'importance: il doit être défini “aire à gauche” (la matière du poinçon est à gauche si on parcourt le cercle dans le sens défini par la succession de ses points).

Suivent les Wires:

wireset = geometry.getWireSet()
wireset.add( Wire(1, [curveset(1), curveset(2), curveset(3), curveset(4)]) )

Même méthode pour le wire constitué des 4 lignes. Celles-ci sont spécifiées par le tuple python [curveset(1), curveset(2), curveset(3), curveset(4)].

Nous passons au dernier niveau pour un test 2D, la Side:

sideset = geometry.getSideSet()
sideset.add(Side(1,[wireset(1)]))

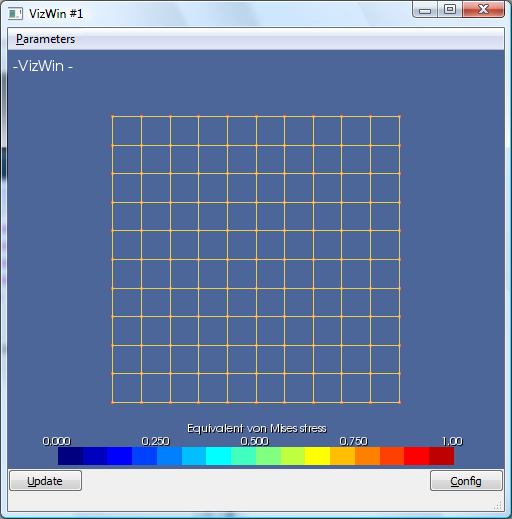
La méthode utilisée est identique (création de l'objet et ajout dans le conteneur correspondant WireSet). A ce stade, il est souvent utile de vérifier si la géométrie est correcte. Pour ce faire, l'utilisateur de Metafor possède les outils de visualisation du module wrap (que nous avons importés au début du fichier). Il suffit d'ajouter ces lignes:

if 1:
    win = VizWin()
    win.add(pointset)
    win.add(curveset)
    win.open()

de lancer metafor et d'importer le module (ou le charger à l'aide de l'interface graphique):

import apps.qs.tutorial

On a créé un objet de type VizWin (fenêtre graphique) nommé win. On y ajoute ensuite ce qu'on veut visualiser (ici, les points et les curves). La fonction open() ouvre la fenêtre.

Nous avons mis ces objets dans un “bloc if” facile à activer et désactiver (il suffit de remplacer le 1 par 0 pour supprimer l'affichage tout en gardant la possibilité de le réactiver plus tard).

Une autre manière de vérifier la géométrie est l'utilisation de la fonction print. Par exemple, print geometry donne un résumé du contenu de la géométrie.

Maillage

Nous passons maintenant au maillage de la géométrie. Puisque Metafor définit la totalité des conditions aux limites sur la géométrie, il serait tout à fait possible de mailler la structure à la fin du module. L'utilisateur doit bien comprendre qu'il ne sera jamais amené à manipuler ni le maillage ni des noeuds ni des éléments. Il est toujours beaucoup plus intelligent de se référer toujours à la géométrie utilisateur. En effet, le nombre de mailles est généralement le paramètre que l'on modifie en premier lieu (pour vérifier la solution obtenue). Si certaines commandes se réfèrent directement à des numéros de noeuds ou de mailles, elles devront être modifiées chaque fois qu'on modifie le maillage. Tout ceci donc pour dire que ce que nous allons faire pourrait se faire à un autre endroit dans le module.

SimpleMesher1D(curveset(1)).execute(n1)
SimpleMesher1D(curveset(2)).execute(n2)
SimpleMesher1D(curveset(3)).execute(n1)
SimpleMesher1D(curveset(4)).execute(n2)
TransfiniteMesher2D(sideset(1)).execute(True)

A ce stade, il faut savoir que, pour accéder à un objet dans un ensemble, il faut utiliser l'opérateur parenthèse (la seule exception est la liste des matériaux qui est un vieil objet Oofelie et qui utilise toujours les crochets). On obtient donc une référence vers la courbe numéro 2 en tapant curveset(2).

Les mailleurs (1D Meshers (Curves), 2D Meshers (Surfaces)) sont associés à l'entité que l'on veut mailler et exécutés par la commande execute(). Pour la face 1, nous utilisons le mailleur intégré MIT (Méthode d'Interpolation Transfinie) qui convient pour des faces à topologie quadrangulaire dont le nombre d'éléments des lignes en vis-à-vis est égal.

Tout comme nous avons vérifié la géométrie utilisateur, il est possible de vérifier visuellement la géometrie du maillage en créant une fenêtre VizWin de la manière suivante:

if 1:
  win = VizWin()
  win.add(geo.getMesh().getPointSet())
  win.add(geo.getMesh().getCurveSet())
  win.open()
  raw_input()

La géométrie à afficher est appelée “mesh” (la géométrie du maillage contient aussi les relations de voisinage).

Il est possible également d'utiliser la fonction print pour afficher la liste des mailles, des arêtes et des sommets.

Définition des éléments volumiques

Nous allons maintenant définir la physique du problème en commençant par informer le domaine des entités physiques (éléments finis) à associer au maillage. Dans ce cas-ci, nous voulons des éléments de volume 2D sur les mailles qui viennent d'être créées.

Materiau

Définissons tout d'abord le comportement volumique du bloc. Ceci peut être fait par la définition de matériaux. L'ensemble des matériaux du problème se trouve dans le domaine.

materialset = domain.getMaterialSet()
materialset.define (1, EvpIsoHHypoMaterial)
materialset(1).put(MASS_DENSITY,     8.93e-9)
materialset(1).put(ELASTIC_MODULUS, 200000.0)
materialset(1).put(POISSON_RATIO,        0.3)
materialset(1).put(YIELD_NUM,             1)

Nous avons également besoin d'une loi d'écrouissage (à définir dans l'ensemble des lois d'écrouissages (MaterialLawSet qui se trouve également dans le domaine):

lawset = domain.getMaterialLawSet()
lawset1 = lawset.define (1, LinearIsotropicHardening)
lawset1.put(IH_SIGEL, 400.0)
lawset1.put(IH_H,    1000.0)

On constate que créer un matériau revient à utiliser la fonction define() de MaterialSet en fournissant le numéro et le type du matériau (ici, c'est un matériau élasto-plastique nommé EvpIsoHHypoMaterial).

Une référence vers l'objet créé dans son ensemble peut être récupérée à l'aide de l'opérateur “parenthèse” (materialset1 = materialset(1)), mais notons aussi que la fonction define() renvoie cette même référence. On utilise alors la fonction membre “put()” du matériau pour définir l'ensemble des paramètres requis (module de Young, densité, etc).

En particulier, on a associé une loi d'écrouissage grâce au code YIELD_NUM). cette loi est définie de manière similaire à un matériau dans l'ensemble MaterialLawSet. Les paramètres sont ici une limite élastique (IH_SIGEL) et un taux d'écrouissage linéaire (IH_H). Chaque matériau et loi ont des codes qui leur sont propres.

Propriétés élémentaires

Avant de définir les éléments finis, on a besoin de créer un objet "propriétés élémentaires" (objet ElementProperties) pour associer les futurs éléments au matériau que nous venons de créer:

prp1 = ElementProperties(Volume2DElement)
prp1.put(MATERIAL, 1)
prp1.put(CAUCHYMECHVOLINTMETH, VES_CMVIM_SRIPR)

On en profite pour spécifier à ce niveau qu'on veut effectuer une sous-intégration sélective de type SRI avec report de pression pour éviter le locking. La définition d'un ElementProperties permet de spécifier le type d'élément volumique voulu (c'est ici qu'on pourrait par exemple un élément thermomécanique au lieu de l'élément mécanique Volume2DElement).

Générateur d'éléments - le FieldApplicator

Il faut enfin ajouter un générateur d'éléments (on appelle ce type d'objet “interaction” dans Metafor). Le générateur d'éléments volumique s'appelle FieldApplicator:

app = FieldApplicator(1)
app.push(sideset(1))
app.addProperty(prp1)
interactionset = domain.getInteractionSet()
interactionset.add(app)

Le FieldApplicator a un numéro et s'ajoute dans l'objet InteractionSet du domaine. Il est nécessaire de spécifier l'entité géométrique maillée sur laquelle vont être créés les futurs éléments finis. La création des éléments est toujours associée à une entité géométrique du problème. On ne va donc pas appliquer les EF sur les mailles mais plutôt sur la géométrie utilisateur. Les liens entre mailles et EF seront effectués en interne dans Metafor.

Le lien entre l'interaction et le ElementProperties se fait avec la commande addProperty().

Pour voir si tout s'est bien passé, il est peut être utile d'effectuer un “print interactionset” pour afficher le contenu de l'ensemble des interactions du domaine. Pour plus de détails, voir Volume interaction.

Conditions limites : Fixations & déplacements imposés

Fixations

Passons aux conditions aux limites. L'ensemble gérant les commandes de condition limites est le LoadingSet (ensemble des chargements).

Nous voulons fixer la composante X de la ligne 4 et la composante Y de la ligne 1 (plans de symmétrie).

loadingset = domain.getLoadingSet()
loadingset.define(curveset(4), Field1D(TX,RE))
loadingset.define(curveset(1), Field1D(TY,RE))

Dans ces commandes, L'objet Field1D passé en argument est un code qui désigne le degré de liberté qu'on veut fixer. En particulier, TX,RE signifie “Translation selon X”, valeur RElative; c'est-à-dire le déplacement.

Chargements (déplacement non nul, charge statique appliquée, ...)

Dans l'exemple, on a besoin de décrire la manière dont le poinçon va bouger au cours du temps. Pour cela, on définit une fonction de type d=f(t). La classe PieceWiseLinearFunction permet de générer des fonctions linéaires par morceau:

fct = PieceWiseLinearFunction()
fct.setData(0.0, 0.0)
fct.setData(1.0, 1.0)

Le déplacement se définit grace à l'ensemble LoadingSet du domaine:

loadingset.define(curveset(5), Field1D(TY,RE),  -0.4, fct)

La création des fixations et des déplacements suit le même schéma que la définition des points de la géométrie: une seule commande define() suffit. Ici, pour les déplacements imposés de notre matrice de contact, on spécifie l'entité (curveset(5) = courbe 5), la direction (TY,RE = déplacement selon y), l'amplitude (-0.4) et l'évolution temporelle (référence à la fonction fct). Le mouvement final sera d(t) = -0.4 * fct(t) = -0.4 * t.

Contact

Le contact est géré par des éléments de contact. Il faut donc définir un nouvel ensemble d'éléments exatement de la même manière que ce que nous avons fait pour les éléments volumiques; c'est-à-dire la définition d'un matériau de contact, un ElementProperties et un générateur d'éléments (une interaction).

Le matériau (matériau #2 dans le MaterialSet) définit un contact collant:

materialset.define(2, StickingContactMaterial)
materialset(2).put(PROF_CONT,    0.05)
materialset(2).put(PEN_TANGENT,  10000)
materialset(2).put(PEN_NORMALE, 10000)

On crée ensuite des propriétés élémentaires pour lier le matériau aux futurs éléments et définir le type d'éléments à générer (Contact2DElement).

prp2 = ElementProperties(Contact2DElement)
prp2.put (MATERIAL, 2)

Il existe plusieurs générateurs d'éléments de contacts. Ici, nous voulons un contact entre une entité rigide (le poinçon) et une entité déformable (le solide maillé). Le générateur correspondant s'appelle RdContactinteraction (RD pour Rigid-Defo):

ci = RdContactInteraction(2)
ci.setTool(curveset(5))
ci.push(curveset(3))
ci.addProperty(prp2)
interactionset.add(ci)

l'objet déformable est spécifié par un push() et l'entité rigide par setTool().

Notons que l'interaction de contact étant ajouté à l'InteractionSet, son numéro DOIT être différent de celui du FieldApplicator (les deux objets sont des interactions…).

Paramètres de l'intégration temporelle

La description du modèle étant terminée, nous allons maintenant nous occuper de la manière dont l'analyse Metafor, qui lancera et pilotera le calcul, va intégrer les équations.

Beaucoup d'options sont disponibles et nous nous limitons ici au minimum, c'est-à-dire à un test quasi-statique (les forces d'inertie sont négligées). Il reste à spécifier l'espace temporel qui nous intéresse et la manière d'archiver les résultats (voir Managing Time Steps).

tsm = metafor.getTimeStepManager()
tsm.setInitialTime(0.0, 0.01)
tsm.setNextTime(1.0, 1, 1.0)

On utilise le gestionnaire de pas de temps (objet TimeStepManager) de Metafor pour spécifier le temps initial (t=0) et le pas de temps initial (dt=0.01s). Ceci-ci initialisera la gestion du pas de temps automatique. La commande setNextTime() est ensuite utilisée pour spécifier les étapes suivantes du calcul (ici, une seule) avec le temps final (t=1s), le nombre d'archivages sur disque voulus (un seul en plus du temps initial - on aura donc 2 archivages) et le pas de temps maximum pour cette période (dt=1.0).

mim = metafor.getMechanicalIterationManager()
mim.setMaxNbOfIterations(7)
mim.setResidualTolerance(1.0e-4)

Nous faisons appel ensuite à l'objet MechanicalIterationManager (voir Managing N.-R. Iterations) qui permet de paramétrer l'algorithme de Newton-Raphson utilisé lors de la résolution des équations d'équilibre. On utilise 7 itérations au maximum et une tolérance de 1.0e-4 (c'est la valeur par défaut).

Extraction de courbes

Si on veut aller plus loin, il est possible de définir également des courbes de résultats sauvées sur disque (variation temporelle de valeurs définies sur la géométrie).

valuesmanager = metafor.getValuesManager()
valuesmanager.add(1, MiscValueExtractor(metafor,EXT_T),'time')
valuesmanager.add(2, DbValueExtractor(curveset(1), Field1D(TY,GF2)), SumOperator(), 'force')

Ces courbes peuvent être visualisées dans VizWin (c'est-à-dire en temps réel, pendant que le calcul tourne) – voir Viewing curves in real time.

La première ligne va chercher le gestionnaire de courbes dans l'analyse Metafor.

La ligne suivante définit la courbe numéro 1 qui va archiver la valeur du temps à chaque pas de temps.

On définit ensuite une courbe (de numéro arbitraire 2) qui extrait la valeur Field1D(TY,GF2) (forces externes) en chaque noeud, en fait la somme et l'écrit sur le fichier nommé force.

Lancer le calcul

Le calcul se charge par load('apps.qs.tutorial') si le module est nommé “tutorial.py” et se trouve dans le répertoire apps/qs. Ensuite, on démarre l'intégration par meta().

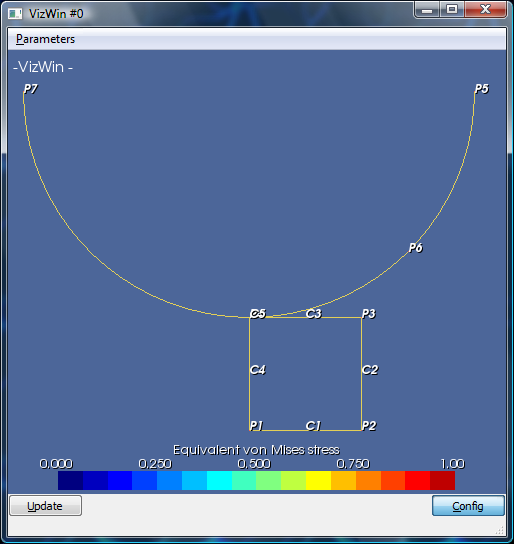
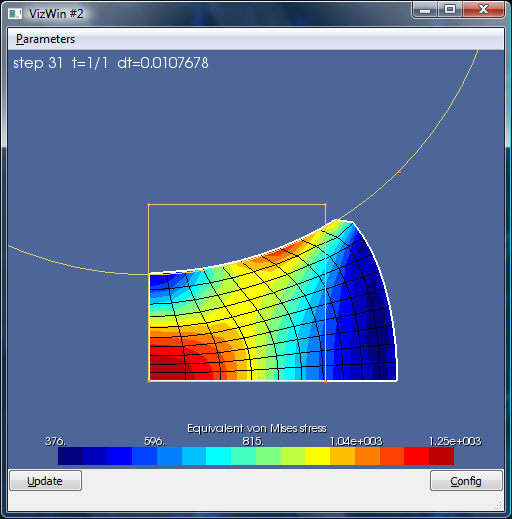
On obtient la célèbre figure suivante:

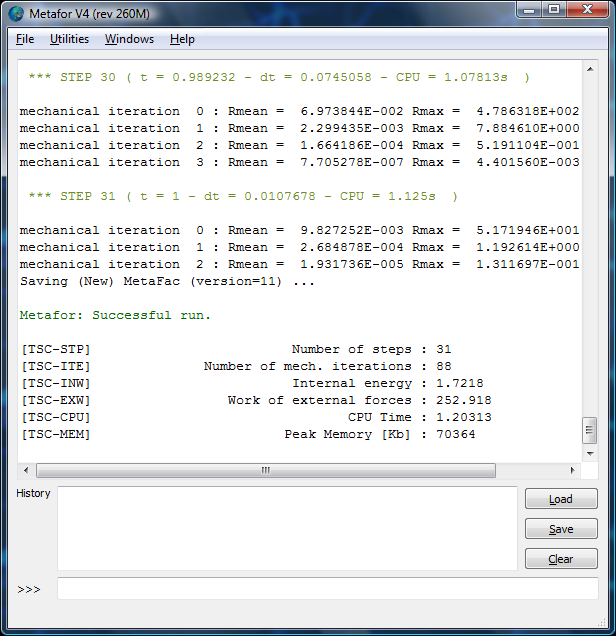
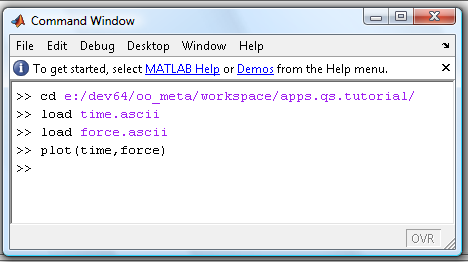
Tandis que la fenêtre python nous indique le bon déroulement de l'intégration temporelle:

Visualiser les résultats

Recharger les configurations sauvegardées

Grâce à VizWin et la visualisation en temps réel, il est possible de voir à tout moment l'état du calcul. Pendant celui-ci, des fichiers d'archivage (.bfac.gz) sont régulièrement créés et peuvent être relus par la suite.

Pour plus de détails sur la procédure, voir How to run an existing test?.

Les courbes sous Excel

Ouvrez Excel et chargez les fichiers .ascii voulus (time.ascii et force.ascii par exemple). Lors de l'ouverture, utilisez le filtre “Tous les fichiers *.*”.

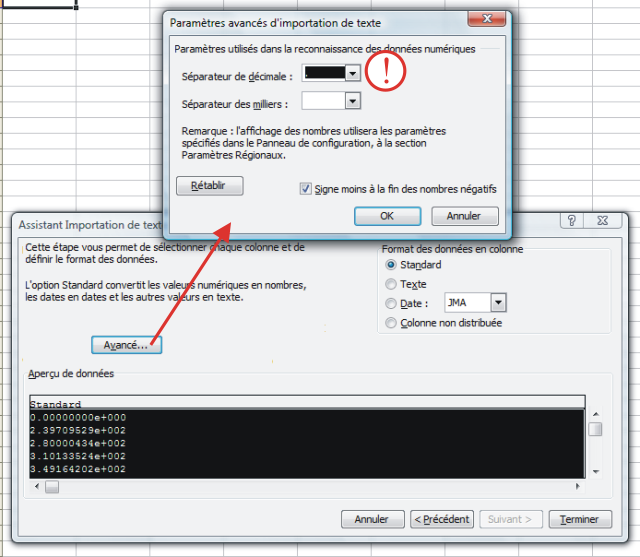
Une boite de dialogue s'ouvre pour configurer l'importation. Il est important de vérifier à ce niveau que le point “.” est bien le séparateur de décimales (voir figure ci-dessous):

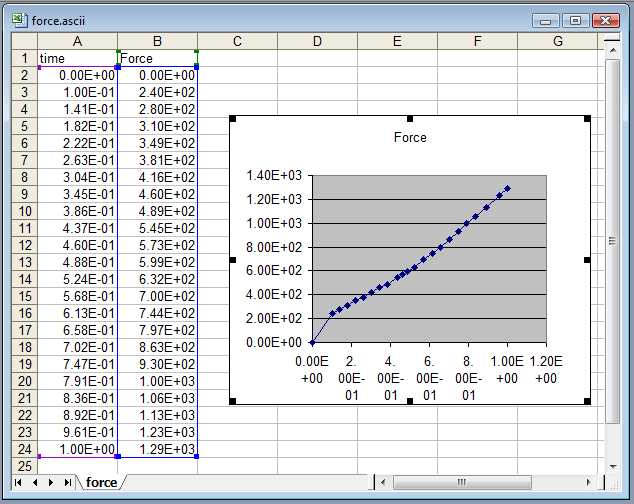
Une fois les deux fichiers importés, placez les deux colonnes dans une seule feuille de calcul et définissez un graphique 2D en sélectionnant les données.

Le résultat est montré sur la figure suivante:

Les courbes sous Matlab

Sous matlab, c'est beaucoup plus simple:

Lancez matlab et chargez les courbes avec la commande load. Utilisez ensuite la commande plot pour tracer la courbe:

Table of Contents