Table of Contents
Surfaces
Definition
In Metafor, a Surface is used to build a (Side) limited by a Wire.
The surface orientation, defined by its normal, is important in 3D contact.
Plane
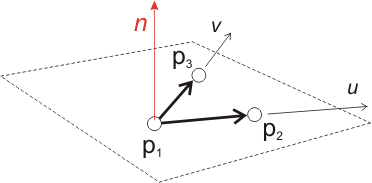
A plane is defined by three points:
plane = surfaceset.add( Plane(number, p1, p2, p3) )
with
number | user number (unique among surfaces and $\ge 1$) |
p1, p2, p3 | the 3 Points lying on the plane |
Its normal (and therefore the surface orientation) is computed using the cross product of vectors $\boldsymbol{p_2}-\boldsymbol{p_1}$ et $\boldsymbol{p_3}-\boldsymbol{p_1}$.
Coons
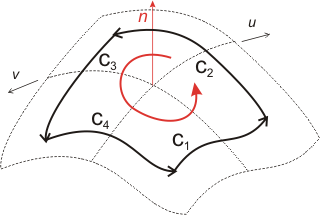
A Coons' surface is a linear interpolation between four Curves. These Curves are gathered in a closed Wire. The Wire orientation defines the surface orientation.
coons = surfaceset.add( Coons(number, wire) )
with
number | user number (unique among surfaces and $\ge 1$) |
wire | the Wire which is interpolated |
Ruled Surface
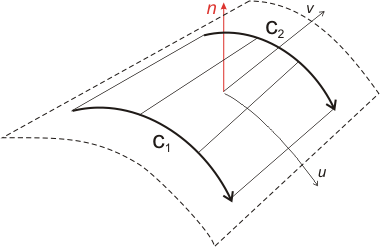
A ruled surface is defined by linearly interpolating two curves. The orientation of these curves sets the surface orientation.
ruled = surfaceset.add( Ruled(number, curve1, curve2) )
with
number | user number (unique among surfaces and $\ge 1$) |
curve1, curve2, … | the 2 facing Curves |
Ruled surfaces can be used to create planes, if the two Curves are coplanar Lines, or cylinders if the curves are Arcs.
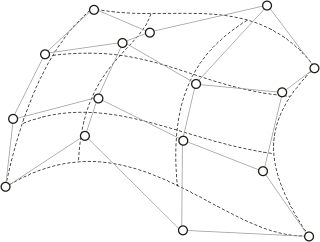
NURBS
nur = surfaceset.add( NurbsSurface(number) ) nur.setDegreeU(degU) nur.setDegreeV(degV) nur.push(i1, j1, p1); nur.pushWeight(i1, j1, w1) nur.push(i2, j2, p2); nur.pushWeight(i2, j2, w2) nur.pushKnotU(knotu1) ... nur.pushKnotU(knotu2) nur.pushKnotV(knotv1) ... nur.pushKnotV(knotv2)
with
number | user number (unique among surfaces and $\ge 1$) |
degU, degV | degree along U and V |
i1, j1, i2, j2, … | indices of the pole matrix |
p1, p2, … | points (called “poles”) |
w1, w2, … | weights |
knotu1, knotu2, … | knot vector along U |
knotv1, knotv2, … | knot vector along V |
Closed Surface of revolution
revsur = surfaceset.add( RevolutionSurface(number, axe, wire) )
with
Open Surface of revolution
openrevsur = surfaceset.add( OpenRevolutionSurface(number, axe, wire, angle) )
with
Sphere
c = Sphere(number, centerPoint, radius, reversed)
with
number | user number (unique among surfaces and $\ge 1$) |
centerPoint | sphere center (Point previously defined in the Pointset !) |
radius | sphere radius |
reversed | unit normal convention - By default (reversed = false), the local covariant tangents are oriented in such a manner that the unit normal points inwards ! |
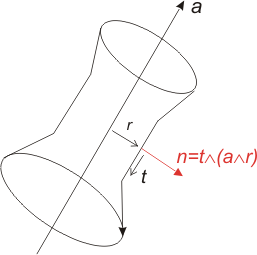
Cylinder
c = Cylinder(number, axis, radius, ptGen) # First way to use Cylinder c = Cylinder(number, axis, radius) # Second way to use Cylinder c.setProjType(projType)
with
number | user number (unique among surfaces and $\ge 1$) |
axis | Line which defines the cylinder axis |
radius | cylinder radius |
ptGen | optional Point of the generating line of the cylinder. This point must be situated: - in a plane perpendicular to the axis including the first point of the axis, - to a distance equal to the cylinder radius of the first point of the axis. Since this point is quite difficult to define when the cylinder is not parallel to an axis, a random point can be supplied and Metafor will put it in its right place with a WARNING_MESSAGE (see apps.qs.contactCylProj0Point). This point is compulsory if the cylinder has a given rotation. |
projType | = 0 : the surface is finite and limited by the length of the axis = 1 : the surface is infinite |