This is an old revision of the document!
Table of Contents
Yield Stress
La classe YieldStress gère la contrainte limite du critère de plasticité.
Qu'elle soit plastique (écrouissage isotrope), visco-plastique (additive : Perzyna, multiplicative : Cowper-Symonds ou non naturellement décomposable : ZerilliArmstrong, JohnsonCook, …).
$$ \sigma_{yield} = \sigma_{yield} (\bar{\varepsilon}^{vp}, \dot{\bar{\varepsilon}}^{vp}, grainSize, ...) $$
Lois implémentées dans Metafor.
IsotropicHardening
Afin de simplifier 80% les tests, les classes IsotropicHardening (Isotropic hardening) sont des (dérivent de) YieldStress.
$$ \sigma_{yield} = \sigma_{isoHard}( \bar{\varepsilon}^{vp}) $$
L'écrouissage isotrope est donc référencié dans le matériau directement comme YieldStress
GsIsoHYieldStress
Contrainte limite définie par un écrouissage isotrope : $$ \sigma_{yield} = \sigma_{isoHard}( \bar{\varepsilon}^{vp}) + \sigma_{grainSize}( \bar{\varepsilon}^{vp}, \dot{\bar{\varepsilon}}^{vp}, grainSize ) $$
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| Numéro de la loi d'écrouissage isotrope | YIELD_NUM | |
| Numéro de la loi d'évolution de la taille de grain | GS_NUM |
PerzynaYieldStress
Contrainte limite définie par un écrouissage isotrope additionné d'une contrainte visco-plastique de Perzyna : $$ \sigma_{yield} = \sigma_{isoHard}( \bar{\varepsilon}^{vp}) + K (\dot{\bar{\varepsilon}}^{vp})^M \left(\bar{\varepsilon}^{vp}\right)^N $$
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| Numéro de la loi d'écrouissage isotrope | YIELD_NUM | |
| $K $ | PERZYNA_K | TM/TO |
| $M $ | PERZYNA_M | TM/TO |
| $N $ | PERZYNA_N | TM/TO |
GsPerzynaYieldStress
Contrainte limite définie par un écrouissage isotrope additionné d'une contrainte visco-plastique de Perzyna et d'une contrainte “taille de grain”: $$ \sigma_{yield} = \sigma_{isoHard}( \bar{\varepsilon}^{vp}) + K (\dot{\bar{\varepsilon}}^{vp})^M \left(\bar{\varepsilon}^{vp}\right)^N + \sigma_{grainSize}( \bar{\varepsilon}^{vp}, \dot{\bar{\varepsilon}}^{vp}, grainSize ) $$
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| Numéro de la loi d'écrouissage isotrope | YIELD_NUM | |
| Numéro de la loi d'évolution de la taille de grain | GS_NUM | |
| $K $ | PERZYNA_K | TM/TO |
| $M $ | PERZYNA_M | TM/TO |
| $N $ | PERZYNA_N | TM/TO |
JohnsonCookYieldStress
Loi visco-plastique de Johnson-Cook :
$$\sigma_{yield}= \left( A+B \left( \bar{\varepsilon}^{vp} \right)^n \right) \left(1+C\ln\left(\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)+C_2\left(\ln\left(\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)\right)^2\right) \left( 1- \left( \dfrac{T-T_{room}}{T_{melt}-T_{room}} \right)^m \right) $$
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| $A $ | JC_A | TM/TO |
| $B $ | JC_B | TM/TO |
| $n $ | JC_N | TM/TO |
| $m $ | JC_M | TM/TO |
| Température de référence $T_{room}$ | JC_TROOM | TM/TO |
| Température de fusion $T_{melt}$ | JC_TMELT | TM/TO |
| $C $ | JC_C | TM/TO |
| $C_2 $ | JC_C2 | TM/TO |
| $\dot{\varepsilon}_0$ | JC_EPSP0 | TM/TO |
JohnsonCookMecYieldStress
Version “isotherme” de la loi visco-plastique de Johnson-Cook :
$$ \sigma_{yield}= \left( A+B \left( \bar{\varepsilon}^{vp} \right)^n \right) \left(1+C\ln\left(\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)+C_2\left(\ln\left(\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)\right)^2\right) $$
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| $A $ | JC_A | TM/TO |
| $B $ | JC_B | TM/TO |
| $n $ | JC_N | TM/TO |
| $C $ | JC_C | TM/TO |
| $C_2 $ | JC_C2 | TM/TO |
| ${\dot\varepsilon}_{0}$ | JC_EPSP0 | TM/TO |
PowJohnsonCookYieldStress
Variante en puissance à la loi visco-plastique de Johnson-Cook (implémentation PP):
$$ \sigma_{yield}= \left( A+B \left( \bar{\varepsilon}^{vp} \right)^n \right) \left(1+\dfrac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\varepsilon}_0}\right)^C \left( 1- \left( \dfrac{T-T_{room}}{T_{melt}-T_{room}} \right)^m \right) $$
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| $A $ | JC_A | TM/TO |
| $B $ | JC_B | TM/TO |
| $n $ | JC_N | TM/TO |
| $m $ | JC_M | TM/TO |
| Température de référence $T_{room}$ | JC_TROOM | TM/TO |
| Température de fusion $T_{melt}$ | JC_TMELT | TM/TO |
| $C $ | JC_C | TM/TO |
| $\dot{\varepsilon}_0$ | JC_EPSP0 | TM/TO |
ZerilliArmstrongYieldStress
Loi visco-plastique de Zerilli-Armstong:
$$ \sigma_{yield} = \sigma_0 + C_5 \left( \bar{\varepsilon}^{vp} \right) ^{n_1} + C_2 \left( \bar{\varepsilon}^{vp} \right)^{n_2} \exp \left( -C_3 T + C_4 T \ln \dot{\bar{\varepsilon}}^{vp} \right) $$
Dans le cas de métaux FCC, prendre $C_5=0$. Dans le cas de métaux BCC, prendre $n_2=0$.

Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| $\sigma_0$ | ZA_SIGMA0 | TM/TO |
| $C_5$ | ZA_C5 | TM/TO |
| $n_1$ | ZA_N1 | TM/TO |
| $C_2$ | ZA_C2 | TM/TO |
| $n_2$ | ZA_N2 | TM/TO |
| $C_3$ | ZA_C3 | TM/TO |
| $C_4$ | ZA_C4 | TM/TO |
CowperSymondsYieldStress
Loi visco-plastique de Cowper-Symonds.
$$ \sigma_{yield}= \sigma_0 \left( 1 + \dfrac{\dot{\overline{\varepsilon}}^{vp}}{D} \right)^{\frac{1}{p}} $$
où $\sigma_0$ est la limite élastique courante dont l'évolution est donnée par une loi de comportement statique (souvent linéaire par morceaux).
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| Numéro de la loi d'écrouissage | YIELD_NUM | |
| $D $ | CS_D | TM/TO |
| $p $ | CS_P | TM/TO |
ViscoKocksMeckingYieldStress
Description
Extension visco-plastique de la loi d'écrouissage isotrope type “Kocks-Mecking”.
$$ \sigma_{y} = \sigma_{y}^{0} + \sigma_{v} [1-exp(-\frac{\Theta_{0}}{\sigma_{v}} \bar{\varepsilon}^{vp}) ] \;\;\; si \;\;\; \sigma_{y} \leq \sigma_{y}^{tr} $$
$$ \sigma_{y} = \sigma_{y}^{tr} + \Theta_{IV} \left( \bar{\varepsilon}^{vp} - \bar{\varepsilon}^{vp}_{tr}\right) \;\;\; si \;\;\; \sigma_{y} > \sigma_{y}^{tr} $$
avec la contrainte limite de transition entre les stades 3 et 4 (déterminée pour assurer une transition continue entre l'écrouissage saturant et constant)
$$ \sigma_{y}^{tr} = \sigma_{y}^{0} + \sigma_{v}\frac{(\Theta_{0}-\Theta_{IV})}{\Theta_{0}} $$
et la défo plastique de transition correspondante :
$$ \bar{\varepsilon}^{vp}_{tr} = \frac{\sigma_{v}}{\Theta_{0}} \ln \left(\frac{\Theta_{0}}{\Theta_{IV}}\right) $$
La composante visqueuse de la contrainte limite se trouve cachée dans le calcul de la contrainte de saturation :
$$ \sigma_{v} = \sigma_{v0} \left ( \frac{\dot{\bar{\varepsilon}}^{vp}}{\dot{\bar{\varepsilon}}^{vp}_{0}} \right ) ^{\left (\frac{kT}{A} \right )} $$
$k$ : constante de Boltzman = $1.381e-23 \mbox{J}/\mbox{K}$
$T$ : Température K (ATTENTION en Kelvin : nécessite de définir la température dans le matériau)
$A$ : Energie d'activation (constante matériau)
${\dot{\bar{\varepsilon}}^{vp}_{0}}$ : référence plastic strain rate (= $1.e7$)
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| $\sigma_0$ | IH_SIGMA0 | TM/TO |
| $\Theta_{0}$ | KM_THETA0 | TM/TO |
| $\Theta_{IV}$ | KM_THETA4 | TM/TO |
| $\sigma_{v0}$ | KM_SIGV0 | - |
| ${\dot{\bar{\varepsilon}}^{vp}_{0}}$ | KM_DEVPL0 | - |
| $k$ : Constante de Boltzman | KM_BOLTZMANN | - |
| $A$ | KM_A | - |
ViscoKocksMecking2YieldStress
Description
Extension visco-plastique de la loi d'écrouissage isotrope type “Kocks-Mecking”. Version 2 pour une meilleur concordance avec le Ta6V Pas de stade 4
L'équation de base reste : $$ \sigma_{y} = \sigma_{y}^{0} + \sigma_{v} \left [1-exp \left (-\frac{\Theta_{0}}{\sigma_{v}} \bar{\varepsilon}^{vp}\right ) \right ] $$
La dépendance à la vitesse de déformation plastique et la température se trouve cachée dans le calcul de la contrainte de Voce $\sigma_{v}$. Tracant la contrainte de Voce en fonction d'un paramètre g défini par :
$$ g = \frac{kT}{\mu b^3} \ln \left ( \frac{\dot{\bar{\varepsilon}}^{vp}_{0}}{\dot{\bar{\varepsilon}}^{vp}} \right ) $$
$b$ : étant la norme du vecteur de Burgers
$k$ : étant la constante de Boltzmann
(pour le Ta6V $ \frac{k}{b^3} ~ 1.135 $ en unité “$\mbox{Mpa}$”)
$T$ : Température K (ATTENTION en Kelvin : nécessite de définir la température dans le matériau)
$\mu$ : Module de cisaillement élastique du matériau (nécessite de redéfinir Young et Poisson dans la loi KM2!!!)
$\dot{\bar{\varepsilon}}^{vp}_{0}$: référence plastic strain rate (= $1.e7$)
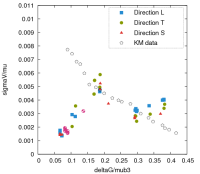
On obtient la figure suivante :
Normalement KocksMecking prédit une évolution linéaire (KM data). Or les données d'essais du Ta6V sont les points colorés. On a donc une évolution en ligne brisée que l'on défini comme suit :
Soit g12 et g23 : valeur de g transition entre les 3 zones :
$$ \frac{\sigma_{v}}{\mu} = A1 \; g + B1 \;\;\;si\;\;\; g < G12 \\ \frac{\sigma_{v}}{\mu} = A2 \; g + B2 \;\;\;si\;\;\; G12 < g < G23 \\ \frac{\sigma_{v}}{\mu} = A3 \; g + B3 \;\;\;si\;\;\; G23 < g $$
Enfin On a aussi observé que l'entrée en plasticité dépend aussi de la vitesse de défo et de la température : (ici, la dépendance de la température est définie explicitement, mais elle pourrait aussi être définie implicitement)
$$\sigma_0 = A + B T + (C + D T) \ln \left (\dot{\bar{\varepsilon}}^{vp}\right ) $$
Paramètres
| Nom | Codes Metafor | Type de dépendance |
|---|---|---|
| $ A $ | IH_SIGEL_A | - |
| $ B $ | IH_SIGEL_B | - |
| $ C $ | IH_SIGEL_C | - |
| $ D $ | IH_SIGEL_D | - |
| $ A1 $ | KM2_SIGVOCE_A1 | - |
| $ B1 $ | KM2_SIGVOCE_B1 | - |
| $ G12 $ | KM2_SIGVOCE_G12 | - |
| $ A2 $ | KM2_SIGVOCE_A2 | - |
| $ B2 $ | KM2_SIGVOCE_B2 | - |
| $ G23 $ | KM2_SIGVOCE_G23 | - |
| $ A3 $ | KM2_SIGVOCE_A3 | - |
| $ B3 $ | KM2_SIGVOCE_B3 | - |
| $\frac{k}{b^3}$ | KM2_BOLTZMANN_BURGER3 | - |
| Module de Young | KM2_ELASTIC_MODULUS | - |
| Coefficient de Poisson | KM2_POISSON_RATIO | - |
| $\Theta_{0}$ | KM_THETA0 | TM/TO |
| ${\dot{\bar{\varepsilon}}^{vp}_{0}}$ | KM_DEVPL0 | - |