Table of Contents
eXtended Finite Element Method
Introduction
Les éléments finis enrichis définis dans la librairies mtXFEM ne permettent pour le moment que de modéliser des discontinuités matérielles de type “material / void”. Les enrichissements spécifiques pour la description d'inclusion, de bi-matériaux ou de phénomènes de fracturation ne sont pas encore disponibles pour les XFEMElements (voir les ElementXFEM défis par Lara dans oo_nda\intelSig\src et bon courage !).
Principe
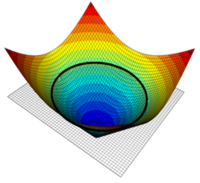
La frontière de la structure est décrite par l’iso-zéro d’une level set (fonction distance signée - cf l’exemple si dessous pour une frontière circulaire). Dans les zones ou la level set est négative, on suppose qu’on est dans la matière, inversement si elle est positive on est dans le vide.
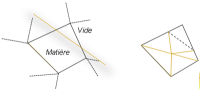
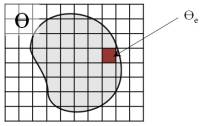
La formulation éléments finis doit donc être enrichie de manière à pouvoir considérer les cas ou l’élément est vide, rempli, ou partiellement rempli. Les deux premiers cas sont triviaux : on les enlève de l’analyse ou on utilise une formulation classique sur l’élément. Pour le dernier cas, on va intégrer par partie les forces internes et la matrice de raideur en utilisant des sous-cellules triangulaires d’intégration.
Ces sous-cellules n’ont pas de degrés de liberté associés. Ce sont uniquement des supports des quantités du quadrangle sur les section de l’élément ou il existe de la matière.
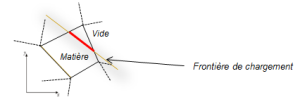
Pour l'application de conditions limites, une stratégie similaire, utilisant des éléments uni-dimensionnels d'intégration, est définie. Elle permet de prendre en compte des chargements sur la frontière de la structure qui sont appliquées à l'intérieur d'un élément fini enrichi.
Intérêt
Les frontières des éléments du maillage n'ont plus besoin d'être coïncidents avec les frontières de la structure. La définition du maillage est alors indépendante de la topologie de la structure.
Quelque soit la complexité de la zone matérielle, une bounding box couvrant l'intégralité du maillage, et dont la qualité géométrique est parfaite, peut alors être utilisée.
Implémentation numérique
Dans Metafor, une nouvelle librairie appelée mtXFEM a permis d'introduire les développements X-FEM indépendamment des librairies déjà existantes pour les éléments finis classique. Une seconde librairie mtXFEMDrawable contient les classes et fonctions d'affichage spécifiques aux X-FEM.
Plus précisement différentes classes ont étés introduites. Les plus importantes sont les suivantes :
- XFEMElement : Élément fini enrichi 2D quadrangulaire. Le fichier cpp est cindé en 3 fichiers :
- XFEMElement_basics : définition numérique de l'élément fini étendu et définition des fonctions “classiques” (constructeur, destructeur, initID, toDofSet, etc.)
- XFEMElement_enrichment : contient toutes les fonctions spécifiques aux éléments finis enrichis (calcul de la fonction level set, construction des éléments d'intégration, etc.)
- XFEMElement_io : contient les fonctions d'affichage (grossièrement copiées-collées du Volume2DElement
- XFEMTractionElement et XFEMContactElement sont les éléments enrichis de chargement. Ils sont bi-dimensionnels (contrairement aux éléments de chargement 2D traditionnels) pour permettre le calcul des quatre forces nodales associées à un chargement interne. Ces deux éléments utilisent respectivement les XFEMLoadingElement et les XFEM1DContactElement comme frontière uni-dimensionnelle d'intégration
- 3 classes d'interactions (XFEMFieldApplicator, XFEMLoadingInteraction, XFEMContactInteraction) dont le fonctionnement est très similaire au fonctionnement des interactions éléments finis classique (voir plus bas).
- Une méthode d'intégration volumique spécifique (XFEMVolumeIntegrationMethod) pour le calcul des quantités aux points de Gauss des sous-cellules d'intégration et des forces internes.
- 3 classes de matériau de contact (XFEMFrictionLessContactMaterial, XFEMStickingContactMaterial, XFEMCoulombContactMaterial)
Formalisme du jeu de données
Différents exemples sont disponibles dans le dossier apps/XFEM/. Le plus simple pour découvrir la syntaxe d'un cas test est de lancer “cont.py”. Ne pas oublier en en-tête de fichier d'importer la libraire mtXFEM et la visualisation en utilisant la commande :
from toolbox.importMetafor_XFEM import *
Définition géométriques
Dans un premier temps on définit une bounding box (rectangulaire, la plus simple possible) de la zone matérielle que l'on va définir par la suite. Cette bounding box sera maillée par la suite en utilisant les outils classiques de Metafor.
Une wire doit par la suite être définie de manière à décrire la frontière initiale de la structure. Cette wire doit éventuellement être orientée selon la méthode de calcul de la level set retenue (voir l'option LS_CALC_METH plus loin).
Enfin des wires permettant de décrire les frontières chargées de la structure (ou suceptible d'être chargées plus tard pour les interactions de contact) doivent être définies.
XFEMFieldApplicator
Tout comme pour les FieldApplicator et autre interactions, il convient de définir dans un premier temps un ElementProperties adéquate pour l'interaction. Les propriétés obligatoires sont les suivantes :
prp1 = ElementProperties(XFEMElement) prp1.put(BOUNDARY_WIRE, 2) # wire décrivant la frontière de la structure prp1.put(CAUCHYMECHVOLINTMETH, VES_CMVIM_STD) # méthode d'intégration pour les éléments remplis prp1.put(MATERIAL, 1) # loi matériau (domain.getMaterialSet()) définie classiquement
Les paramêtre optionnels sont les suivants. Pour cet exemple les paramètres par défaut sont donnés
prp1.put(NB_IP_INTCELL, 1) # nombre de points de gauss par sous cellule triangulaire prp1.put(INVERSE_WIRE, 0) # Wire décrite vide a droite ou a gauche (pour modéliser des trous) prp1.put(TOL_LEVELSET, 0.15) # % a partir de laquelle la distance signée est mise à zéro prp1.put(LS_CALC_METH, 0) # méthode de calcul du signe de la level set prp1.put(SOUS_INTEG, 0) # méthode apparentée à la sous-intégration pour les éléments coupés prp1.put(FULL_SIDES, 0) # affichage de l'ensemble des éléments ou seulement des actifs
Attention, en fonction des paramêtres LS_CALC_METH et TOL_LEVELSET, la définition du maillage de calcul peut parfois échouer. En agissant sur ces deux paramêtres il est souvent possible de retrouver un maillage de calcul correct.
Une fois l'ElementProperties correctement définit, le XFEMFieldApplicator est définit classiquement (comme un FieldApplicator classique) :
app = XFEMFieldApplicator(1) app.push(Sset(1)) # numéro de la side correspondant à la bounding box maillée app.addProperty(prp1) domain.getInteractionSet().add(app)
Interaction de chargement
L'ElementProperties pour une interaction de chargement est le suivant :
prp2 = ElementProperties(XFEMTractionElement) prp2.put(XPRESSURE, 100000000) # Pression de chargement prp2.put(XNIP, 2) # Nombre de point de gauss par cellule linéaire d'intégration
En pratique, il absolument inutile d' utiliser plus de deux points d'intégration (si les éléments sont linéaires). Comme pour les interactions classiques, il est possible de faire dépendre la pression du temps :
fct = PieceWiseLinearFunction() fct.setData(0.0, 0.0) fct.setData(1.0, 1.0) prp2.depend(XPRESSURE, fct, Field1D(TM,RE))
L'interaction de chargement est alors définie de la manière suivante :
load = XFEMLoadingInteraction(2) load.push(Cset(13)) # curve chargée load.addProperty(prp2) domain.getInteractionSet().add(load)
Interaction de contact
Dans un premier temps on définit un matériau de contact, qui permet de définir les paramètres de pénalités. En fonction du matériau de contact retenu, seuls certains paramètres doivent être définis :
Mat.define(2,XFEMFrictionlessContactMaterial) Mat(2).put(NPENALTY, 1.e9) # pénalité normale Mat(2).put(TPENALTY, 3.3e8) # pénalité tangente (sauf pour XFEMFrictionlessContactMaterial) Mat(2).put(COEF_FROT, 0.3) # seulement pour XFEMCoulombContactMaterial Mat(2).put(UNILAT, 0) # loi de contact unilatéral ou non
Seuls deux paramêtres sont définis dans le ElementProperties : la loi de matériau de contact, et le nombre de point de gauss par sous-cellule d'intégration de conditions limites.
prp2 = ElementProperties(XFEMContactElement) prp2.put(MATERIAL, 2) prp2.put(XNIP, 2)
Enfin l'interaction de contact est définie comme une interaction de contact classique (push des frontières suceptibles de rentrer en contact avec l'outil définit par setTool :
load = XFEMContactInteraction(2) load.setTool(Cset(8)) load.push(Cset(5)) load.push(Cset(12)) load.push(Cset(9)) load.addProperty(prp2) domain.getInteractionSet().add(load)
Reste du jeu de données
Le reste du jeu de données est classique. Pour le mechanicalIterationManager, je conseille de mettre la tolérance sur le résidu à 1.0e-2. Dans le cas ou un encastrement est définit en utilisant une XFEMContactIteration (XFEMStickingContactMaterial avec unilatéral nul) il peut être nécessaire de réduire la valeur de cette tolérance.
Affichage
L'affichage classique est remplacé par l'affichage des éléments complètements rempli et par les cellules d'intégration. De manière à mieux visualiser les XFEM je conseille d'utiliser la visualisation suivante :
try :
win1 = VizWin()
win1.add(app.getXFEMSides().getCurveSet())
win1.add(app.getXFEMElementSet())
win1.open()
metafor.addObserver(win1)
except NameError:
pass
et de désactiver l'affichage de la grille (maillage de calcul)dans les options de la fenêtre. La dimension de app.getXFEMSides().getCurveSet() dépend du paramètre FULL_SIDES (affichage du maillage des éléments, ou uniquement des éléments actifs).
Limitations actuelles
- Lorsque le chargement sur la structure devient trop important, la distorsion du maillage pour les éléments peut remplis provoque l'apparition d'un jacobien négatif et l'arrêt du calcul.
- Dans certains cas, le calcul du signe de la fonction level set peut être faux… Dans ce cas la zone matérielle numérique ne correspond pas à la zone matérielle définie par l'utilisateur. L'utilisation du paramètre LS_CALC_METH permet néanmoins de limiter l'apparition de ce problème.
- Des surcontraintes peuvent apparaitre sur les éléments en contact de part le chargement.
- L'utilisation de trop de point de gauss par sous-cellules triangulaire peut provoquer des surcontraintes et l'arrêt du calcul faute de convergence.
- Si la frontière présente deux arrêtes vives au sein d'un unique élément, un seul point de “bifurcation” est détecté par Metafor (il correspond à celui permettant de couvrir la zone matérielle la plus importante).