This is an old revision of the document!
Table of Contents
Evolution function
Functions are quite useful to describe how some parameters evolve, over time for example. They can be used to set displacements or to define hardening laws.
PieceWiseLinearFunction
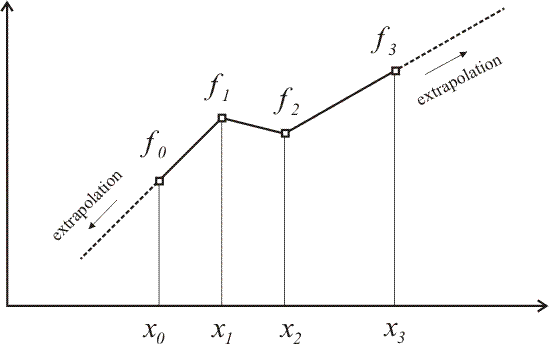
A piecewise linear function is defined one point at a time:
fct = PieceWiseLinearFunction() fct.setData(abs1, ord1) fct.setData(abs2, ord2) ...
where
abs1, abs2, … | list of abscissae |
ord1, ord2, … | list of ordinates |
Remark #1: Evolution functions are objects derived from refCounted. Once associated to a loading, their reference is incremented and memory management is associated to the object which uses them. Therefore, it is no longer required to define them as global.
Remark #2: As can be seen above, the first and last segments are extrapolated if a value of the function is required outside its domain.
PythonOneParameterFunction
If function is too complex to be defined with a PieceWiseLinearFunction, it must be defined analytically, with the function PythonOneParameterFunction.
The goal is to give as argument a Python function as OneParameterFunction.
For example, this is used to:
- Configure the mesher (1D Meshers (Curves)).
- Pilot most metafor objects in a more advanced way (Prescribed Displacements).
- Define a hardening function with Python (General Points).
Example: the ramp function:
fct1 = PieceWiseLinearFunction() fct1.setdata(0,0) fct1.setdata(1,1)
becomes with interpreted Python:
def f(a):
return a
fct1 = PythonOneParameterFunction(f)
or, using python lambda function:
f = lambda x: x fct1 = PythonOneParameterFunction(f)
The value can also be displayed for each estimation, and a more complex function can also be defined using all Python tools. For example, a load function can be first defined with a parabola, then with a straight line, the change between these two being controlled by an conditional structure.
def f(a):
val=0
if(a‹0.5):
val=a*a
else:
x=0.5*0.5;
val=x+(a-0.5)/(1-0.5)*(1-x)
print 'value=', val
return val
fct1 = PythonOneParameterFunction(f)