This is an old revision of the document!
Table of Contents
Automatic Remeshing Process
This page will explain how to use the Finally Efficient and Nicely Redesigned Implementation of Remeshing, aka FENRIR.
Foreword
Although, when bragging about Metafor on posters or conferences, there has always been a rather obscure “Meshing and remeshing procedures” about which we were hoping that nobody would ask questions, now it is actually true, you can finally remesh a (2D) part with Metafor and continue the simulation !
And I am not talking about a tedious, complicated procedure which cannot be used by people without a 200-IQ (or a very strange way of thinking…), but a very simple, straightforward process that even students can try (students, please take no offense, by students I just mean people with a limited knowledge of Metafor, not of course that students are stupid 
Why would I need remeshing ?
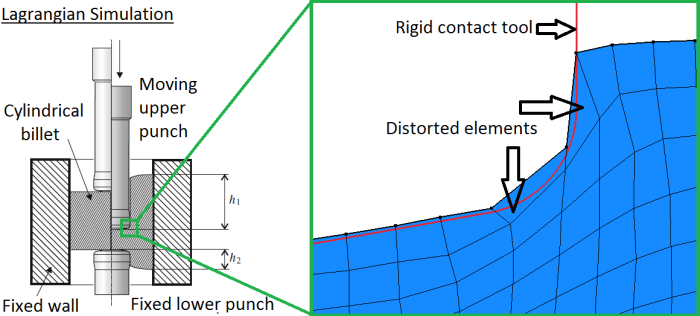
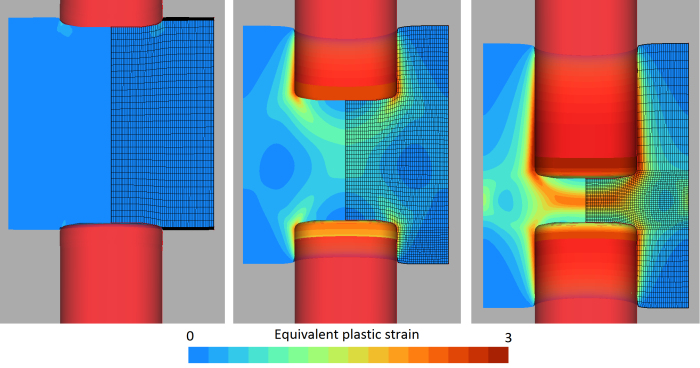
When trying to model metal forming processes, large deformations often lead to significant mesh distortions. Consequently, the quality of the results is deteriorated, until a point where the analysis terminates because of numerical errors. This is illustrated below for the Double Cup Extrusion Test, where we seen that quite soon, some elements are heavily distorted.
A first solution to avoid this process is to use the arbitrary Lagrangian Eulerian formalism (ALE). In very simple terms, using the ALE means that the mesh is not going to move alongside the matter anymore, but will move as the user dictates. It is very powerful for simple geometries where the motion of the mesh is easy to predict, for example the Double Cup Extrusion test :
On this test, on the upper and lower right of the workpiece, two small auxiliary, very thin meshes where constructed, and the are going to extend as the matter flow through them. Once this model is established, it renders the computation very fast and accurate.
However, for more complex geometries, such a formalism is not possible to implement. Consequently, another solution consists in stopping the simulation to remesh the part, transfer data from the old mesh to the new one, and then restart the simulation.
However, doing so manually is at least as tedious as defining a model with the ALE. Imagine : running a computation until it stops because of numerical errors, programming a very complicated remeshing operation a bit before, running again the computation until it stops another time, programming the next remeshing… With this approach, it would take days to define a whole model, and do not even try to think about mesh analysis !
Which is why all of this has been kindly automatized, so that you just have a few settings to define, click on execute, and just sit back, relax, and enjoy the beauty of FENRIR !
How does remeshing work ?
First, you need to have an operational 2D test case, and the will to introduce remeshing into it.
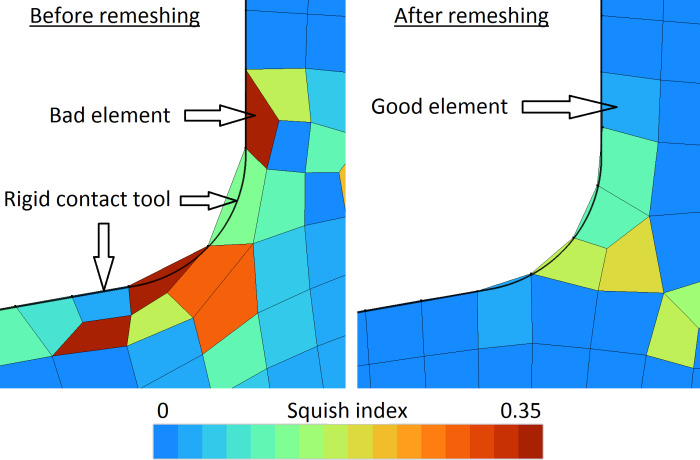
To do so, you have to define a “remeshing criterion”, which is a criterion which, once verified, will trigger remeshing. The chosen criterion really depends on your simulation. You can for example decide that you want to remesh every second, or as soon as a tool has moved 1cm, or when the aspect ratio of your mesh reaches a critical value… This is illustrated below, where the squish index (angular distorsion of the element) is used as a criterion.
Then, this criterion is simply given to the metafor object, along with a maximal value, and the computation can be started. During the integration, at the end of every successful time step, this criterion is computed, compared to the given tolerance, and as soon as it is verified, the time integration is stopped, and the magic starts :
First, the part is remeshed using the oh-so-wonderful Gen4 mesher, and so the old, distorted mesh is replaced by a brand new, distortion-free mesh.
Second, data must be transferred from the old to the new mesh. As you very well know, the Gauss points contains information about strains and stresses, and the nodes about displacements, velocities and temperatures. However, just after remeshing, the newly defined nodes and Gauss points do not know anything, since they were just created ! If we do not want to loose what was computed during the previous time integration, then data (stresses, temperatures, velocities…) must be transferred to the new mesh.
Once this is done (it used to take a bloody hell of a f***ing time, but now the time required is more reasonable, see 01_19 for details), we have a good new mesh, containing data from the previous computation. From this, the simulation can be restarted, which means that the time integration is carried out further, until the remeshing criterion is met again and another remeshing operation takes place.
And that's it for the basics ! But as they say, a picture is worth a thousand words, and I guess that a video is worth a thousand pictures, so just enjoy the following video, about the modelling of forging, to see how it works :
<html>
<iframe width=“640” height=“480” src=“www.youtube.com/embed/TcLghZZCfyA” frameborder=“0” allowfullscreen></iframe></html>
</WRAP>
===== How do I build my own remeshing model ?=====
Fortunately, the whole procedure was designed to be as user-friendly as possible, which means that you have very, very few things to do to adapt an existing model for remeshing ! Indeed, all the implementation of the procedure is hidden in the file toolbox.remeshingUtilities. Feel free to take a look if you want to know how it works, but no pressure.
No, to run FENRIR, you will only need to create two files :
* The first one is the test-case, which you have already. It should be slightly modified to include remeshing.
* The second one is a short script. In it, you will define the settings of your remeshing, for example the remeshing criterion. Basically, this script will give to the routines hidden in toolbox.remeshingUtilities the getMetafor() function from your test case and the few options defined in the script.
Many examples can be found in apps.remeshing2. The subfolder baseTests contains tests slightly modified for remeshing (cont2, forge, ..). The subfolder fullAuto contains the scripts used to run the corresponding base tests. Do not worry about the subfolders semiAuto, manual and nullRemeshing, they are just there to check that nobody (myself included) messes with my algorithms.
==== File 1 : test-case ====
Test-cases modified for remeshing can be found in apps.remeshing2.baseTests. Look at cont2 for the simplest one with the changes annotated.
Before stating the changes, I must point two things out :
* First; all the test-case definition (geometry, mesh, properties, curves…) must be inside a getMetafor() function. It does not work should part of it be defined outside any function (like in apps.tutorials.tutorial1 where all is left aligned).
* Second, the example described below is based on the fact that Gen4 is the only mesher used. You can also used transfinite meshers, but it requires more test-case modifications, which are described further
=== Step 1 : Eliminate Global ===
First, all global metafor should be removed. By global, I mean all lines such as :
* metafor = None
* global metafor
* if metafor: return metafor
The point in setting the object metafor as a global variable was to avoid defining a new Metafor object (which uses a lot of RAM) every time that the function getMetafor is called, so that only one Metafor object is build no matter how many times the function is called. However, in this context, we will need to create a new Metafor object every time that we want to remesh, which is not possible if it was declared as global.
=== Step 2 : Define a getParameters() function ===
This is not compulsory, the procedure was designed so that you only need the getMetafor() function. However, I find more convenient to work with such a function, so all test-cases in the battery have this function. To be consistent, this tutorial will assume the same.
This function, which already exists in most test-cases, will look like
def getParameters(_p={}):
p = {}
# Define parameters
# …
# Initialize remeshing key
p['remeshing'] = None
p.update(_p)
return p
The only change with respect to a classical getParameters() function is the definition of the key remeshing in the Python dictionary used as argument of the function Metafor. When remeshing operations must be carried out, p['remeshing'] will contain an object with all the information required for the remeshing. However, for the first integration (and when we want to read results), we do not want to remesh, so it is set to None.
=== Step 3 : Encapsulate all meshing operations ===
Then, the idea is that your test-case is able, on its own, to define both a traditional domain as well as a remeshed domain (otherwise reading the results after 20 remeshing operations requires to rebuild all 20 corresponding Metafor objects, which is a tiny bit annoying…). Therefore, we have to use a conditional statement to decide whether we want to mesh, or to remesh. Consequently, the traditional structure of a test-case must be changed as shown below :
# Usual | # Remeshing
|
def getMetafor(_p={}): | def getMetafor(_p={}):
metafor = Metafor() | metafor = Metafor()
p = getParameters(_p) | p = getParameters(_p)
|
# Build Geometry | # Build Geometry
# Build Mesh | if not p['remeshing'] or not p['remeshing'].remeshing:
| # Build Mesh
| else:
| # Remesh
# Fill Elements | # Fill Elements
#… | #…
return metafor | return metafor
So that you understand the guardian better, this getMetafor() function can be called in four different situations. We can either :
* Run it with a load/meta (without remeshing)
* Run it with FENRIR, during the first integration, and mesh normally
* Run it with FENRIR, during the others integrations, and remesh
* Read results with a load/loadFac
In the code of the test-case, we do not know which of these is supposed to be done, hence the p['remeshing]. We have the following correspondance :
* p['remeshing] == None means load/meta or load/loadFac
* p['remeshing].remeshing = False means first integration when using FENRIR
* p['remeshing].remeshing = True means the others integrations when using FENRIR
=== Step 4 : Define remeshing ===
Now that we have separated the remeshing part from the meshing one, all that remains is to actually define the remeshing operations. Using Gen4 to remesh the part is simply done with the command :
from toolbox.remeshers import Gen4Remesher
Gen4Remesher(side, p['remeshing'].oldDomain, domain, density).execute()
where :
* side is the side to remesh
* p['remeshing'].oldDomain is the domain of the “old Metafor”, used to get the deformed geometry. You must use this exact syntax.
* domain is the domain of the current Metafor object
* density is the desired mesh density.
If the test cases contains several sides which were meshed separately, then this must be done for each of them.
Remeshers can be combined and different densities can be set for each side.
=== Summary ===
So to summarize, you must :
* remove all global metafor
* Initialise the key remeshing to None in the dictionnary of arguments defined in the getParameters() function
* encapsulate all meshing operations in a conditional structure with the guardian if not p['remeshing'] or not p['remeshing'].remeshing
* define the remeshing operations
The corresponding change can be seen in the pseudo code below :
# Usual | # Remeshing
|
metafor = None |
|
def getParameters(_p={}): | def getParameters(_p={}):
p = {} | p = {}
|
# Define parameters | # Define parameters
# … | # …
|
| # Initialize remeshing key
| p['remeshing'] = None
|
p.update(_p) | p.update(_p)
return p | return p
|
def getMetafor(_p={}): | def getMetafor(_p={}):
global metafor |
if metafor : return metafor |
metafor = Metafor() | metafor = Metafor()
|
p = getParameters(_p) | p = getParameters(_p)
|
# Build Geometry | # Build Geometry
|
# Build Mesh | if not p['remeshing'] or not p['remeshing'].remeshing
| # Build Mesh
| else:
| # Remesh
|
# Fill Elements | # Fill Elements
#… | #…
return metafor | return metafor
==== File 2 : script ====
Now that the test case is ready, a script must be written, in which all remeshing parameters are going to be set. Examples are found in apps.remeshing2.fullAuto. Look at cont2aRemeshing for the simplest one with changes annotated.
So what should this script contain ?
=== Header ===
As for every test case, we must start with the line :
from wrap import *
I mentioned earlier that the remeshing algorithm was hidden in another file, so that you do not have to worry about it.
Obviously, this file must be imported :
from toolbox.remeshingUtilities import AutomaticRemeshing
Then, the base test you just modified must also be imported :
import apps.remeshing2.baseTests.cont2 as test
=== getParameters() ===
It is not compulsory, but is is easier to have a function getParameters. As in traditional test cases, this function simply creates a python dictionary p and fills it with any relevant parameters. For the remeshing algorithm, we can for example define the critical value(s) which will trigger remeshing.
Such a function will look like :
def getParameters(_p={}):
p = test.getParameters(_p) #import parameters from base test
# Change test parameters if desired
# …
p['stopValue'] = 0.25 #set critical value for remeshing
p.update(_p)
return p
=== getMetafor() ===
As always, a getMetafor function is required. This one will will simply call the one from the test-case, define a remeshing criterion, and then add the remeshing criterion to metafor. For example, the following lines define a criterion which will compute the IF_MESH_QUALITY on the side number 1 and trigger remeshing as soon as the value p['stopValue'] is reached.
def getMetafor(_p={}):
p = getParameters(_p)
metafor = test.getMetafor(p)
#Stop Criterion - Value Extractor
sideset = metafor.getDomain().getGeometry().getSideSet()
valueExtr = IFNodalValueExtractor(sideset(1), IF_MESH_QUALITY)
criterion = ValueExtractorStopCriterion(valueExtr)
criterion.setStopValue(p['stopValue'])
metafor.setStopCriterion(criterion)
return metafor
=== main() ===
Finally, a main function should be defined, in which all remeshing, data transfer and balancing properties are set. This will look like :
def main():
load(name)
autoRemesh = AutomaticRemeshing(getMetafor, file)
autoRemesh.setInteractionToTransfer(99)
autoRemesh.setInteractionToPostStep(1)
autoRemesh.setBalancing(True)
autoRemesh.makeAnim = False
autoRemesh.execute()
if name == “main”:
main()
This is pretty straightforward :
* the AutomaticRemeshing object takes two arguments, a getMetafor function handle, and the file name (to define the right workspace).
* setInteractionToTransfer gives to FENRIR the user number of the interaction you want to transfer, here number 99.
* setInteractionToPostStep gives to FENRIR the user number of the interaction on which post-remeshing operations should be executed (typically, any contact interaction), here number 1.
* The line autoRemesh.setBalancing(True) is the magical ingredient that makes everything taste better… I will talk more about this in a following section.
* Finally, the line autoRemesh.makeAnim = False indicates that we have no wish to make a save a picture every time that a fac is saved (to make an anim later on). If set to True, then after each time integration, all facs will be loaded and a screenshot will be saved as a .bmp in the folder Anim, located in the workspace, just as is traditionally done when clicking on the button makeAnimation in Metafor GUI.
Now that you have altered your test case to include remeshing, and that you have defined this little script, all that remains is to launch Metafor and execute your script (execute, not load/meta). Everything should work out perfectly.
==== History curves ====
There is one more thing to change in the test-case. If you have followed this tutorial so far, and if your test-case was opening some visualisation windows with some results curves on them, then you have noticed that new windows were opening after each remeshing. This is quite annoying, but with a little bit of reorganization, we can get rid of that.
All that we need to do is encapsulate the part of the test-case where the windows are created in a conditional statement, just like we did for the mesh and remesh part. Here is what this will look like :
# Usual | # Remeshing
|
| if p['remeshing'] == None or p['remeshing'].observers == None:
winc1 = VizWin() | winc1 = VizWin()
winc1.add(dataCurveSet1) | winc1.add(dataCurveSet1)
metafor.addObserver(winc1) | metafor.addObserver(winc1)
| else:
| p['remeshing'].observers[0].clearDrawables()
| p['remeshing'].observers[0].add(dataCurveSet1)
| metafor.addObserver(p['remeshing'].observers[0])
With this statement, the window winc1 displaying the history curve will be created during the first integration, then all the next Metafor objects will use the same windows to plot their curves after remeshing, instead of creating a new window every time.
These windows will be closed automatically when the integration is complete. If you want to keep them open at this point, they should be declared as global objects.
===== Additional features =====
==== Changing the critical remeshing value during the computation ====
It may be possible that we want to change the critical value after a few remeshing (see for example apps.remeshing2.fullAuto.cont2bRemeshing). If you recall, this value is defined in the ''getParameters()'' function of the script.
However, since the same two files are used to generate all the remeshing, it is not possible to know how far in the computation we are. But to change the critical value, we need to know whether the current integration is the first or the tenth.
Consequently, a second special key was introduced in the dictionary of arguments. We already had p['remeshing'], which contains all information required to defined a remeshing, now we also have p['integrationNumber']. p['integrationNumber'] is set to one for the first integration, and will be incremented after each remeshing operation.
For example, if we want to the first remeshing to occur at p['stopValue'] = 0.15, then all others at p['stopValue'] = 0.25, we change the code from above to :
def getParameters(_p={}):
p = test.getParameters(_p)
if 'integrationNumber' not in p.keys():
p['integrationNumber'] = -1 # 1 : initialise the key to -1
# Change test parameters if desired
# …
p.update(_p) # 2 : update the dictionary
if p['integrationNumber'] == 1: # 3 : use value to determine right critical value
p['stopValue'] =0.15
else:
p['stopValue'] =0.25
return p
Please pay attention to the order !
First, if the key integrationNumber is not found in the dictionary (meaning that we are reloading results), we need to initialise it (to -1 to avoid ambiguities), because otherwise we will not be able to load the results.
Then, we must update the dictionary, to replace this value by the correct one given by FENRIR.
Afterwards, p['integrationNumber'] contains the correct value and can be use to choose the right critical value
==== Changing mesh density during the computation ====
Actually, the key p['integrationNumber'] can be used to modify any and all parameters during the computation (see for example apps.remeshing2.fullAuto.cont2bRemeshing). For example, if we want to double the mesh density after two remeshing, we simply add in the getParameters() function of the script (after the update !) :
if p['integrationNumber'] < 3:
p['meshDensity'] = 1.0/20.0
else:
p['meshDensity'] = 1.0/40.0
==== Using other remeshing criteria ===
Two different remeshing criteria have been implemented yet, one based on a ValueExtractor, the other on time.
Previously, the one relying on a valueExtractor was used in a very simple way : on one side of the part, with the field IF_MESH_QUALITY. But is can be used with any ValueExtractor you want, and on any geometrical entity. For example, let us assume that we want a criterion based on the aspect ratio, which is to be evaluated on two different sides. Then we simply define a skin with these two sides and we have the following :
#Stop Criterion
sideset = metafor.getDomain().getGeometry().getSideSet()
skinset = metafor.getDomain().getGeometry().getSkinSet()
skinset.add(Skin (1, [sideset(1), sideset(2)]))
valueExtr = IFNodalValueExtractor(skinset(1), IF_MESH_QUALITY_AR)
criterion = ValueExtractorStopCriterion(valueExtr)
criterion.setStopValue(p['stopValue'])
metafor.setStopCriterion(criterion)
But then, there is also a simple criterion based on time, if you want to remesh every few seconds or so.
In this case, you must first define a vector containing all the times at which you want to remesh (p[stopTime]), then use the key p[integrationNumber] to set the right remeshing time depending on the integration. See below, or see apps.remeshing2.fullAuto.cont2cRemeshing, for the example :
def getParameters(_p={}):
p = test.getParameters(_p)
p['tmax'] = 1.2
if 'integrationNumber' not in p.keys()
p['integrationNumber'] = -1
p['stopTime'] = [0.3, 0.6, 0.8, 1.0, 1.2]
p.update(_p)
return p
def getMetafor(_p={}):
p = getParameters(_p)
metafor = test.getMetafor(p)
#Stop Criterion - Time
criterion = TimeStopCriterion()
criterion.setStopValue(p['stopTime'][p['integrationNumber']-1])
metafor.setStopCriterion(criterion)
return metafor
As you can see, we first defined a table containing the five critical values. Then, when setting the stop value to the criterion, we used this counter p['integrationNumber'] to get the number of the integration and get the appropriate critical value from the table.
===== Meshers =====
==== Gen4Remesher ====
Gen4Remesher is the default mesher used for remeshing. The new boundary of the model is constructed by spline interpolation, to try to reconstruct a new boundary as close to the old one as possible (see below)
 Then, once the boundary is reconstructed, the domain itself is meshed using Gen4, so by recursively splitting it until quadrilateral elements are obtained :
Then, once the boundary is reconstructed, the domain itself is meshed using Gen4, so by recursively splitting it until quadrilateral elements are obtained :
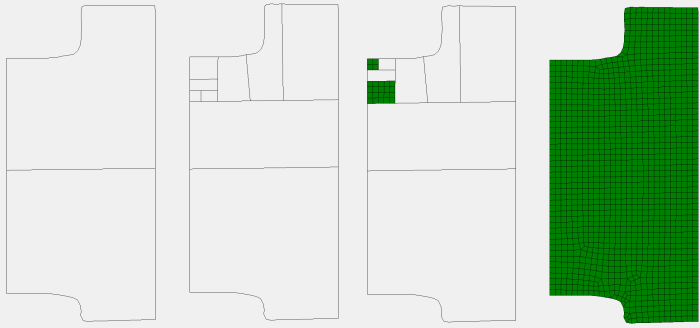 The commands to do so are simply :
from toolbox.remeshers import Gen4Remesher
Gen4Remesher(side, p['remeshing'].oldDomain, domain, density).execute()
where :
*
The commands to do so are simply :
from toolbox.remeshers import Gen4Remesher
Gen4Remesher(side, p['remeshing'].oldDomain, domain, density).execute()
where :
* side is the side to remesh
* p['remeshing'].oldDomain is the domain of the “old Metafor”, used to get the deformed geometry. You must use this exact syntax.
* domain is the domain of the current Metafor object
* density is the desired mesh density.
==== CopyRemesher ====
If the entire domain is to be remeshed, Gen4Remesher is all you need. However, for more complex test cases where only part of the domain is to be remeshed, the CopyRemesher becomes useful. It is a “mesher” which will simply copy the old mesh into the new domain, keeping the exact same nodes and cells. The commands to use it are similar to those of Gen4Remesher :
from toolbox.remeshers import CopyRemesher
CopyRemesher(side, p['remeshing'].oldDomain, domain, density).execute()
Therefore, if you have a complex domain, just divide it into the appropriate sides and copy/remesh as you see fit. However, when you want to remesh one side, copy another side, and that the two sides have a common edge, then you must first use CopyRemesher, then Gen4remesher, in order ensure that the nodes of the edges are also copied and not regenerated !
==== Transfinite Meshers ====
Sometimes, it is useful to first mesh curves using the SimpleMesher1D before meshing the domain itself, in order for example to ensure that some nodes are equidistant (which is not certain when using Gen4 alone). However, at this point, it is not possible to use the SimpleMesher1D for remeshing (again, simply because I never had the use for it). Also, you cannot remesh using Transfinite mesher, simply because I have been able to do all I want with Gen4 and did not take the time to program it. Feel free to do it if you want.
You can, however, use transfinite meshers to define your first, initial mesh. This initial mesh can indeed be created using any configuration of meshers one can think of. However, reading the results afterwards is going to be annoying.
For example, let us assume that TransfiniteMesher2D is used to create the first mesh. Then, for the first integration, no mesh files are saved, so to reload the corresponding facs the mesher must be executed again.
For the others integrations, Gen4Remesher is used, and a mesh file is saved, so reloading the fac means reading the mesh file.
However, when loading a fac, there is no way to know which operations should be done, executing the transfinite mesher or reading the gen4 mesh file. Consequently, the test-case will have to be slightly modified depending on the results you want to read. This is annoying indeed, and could be solve if mesh files were saved for any meshers. In would be interesting to do so, but well…
===== Data Transfer =====
By default, the transfer of data is done using Philippe's complex “FVTM” routine with all its default parameters (see Transfert de données entre deux maillages, in French).
For the advanced user, changing these parameters is possible (in the main() function of the script)
==== Changing the transfer method ====
As mentioned above, the command to transfer the intraction no is setInteractionToTransfer(no). For example,
:
autoRemesh = AutomaticRemeshing(getMetafor, file)
autoRemesh.setInteractionToTransfer(1)
indicates that the interaction 1 is to be transferred with default properties.
By default, the “most advanced” method is used (nicely called “FVTM”, for Finite Volume Transfer Method). If you want to use the more simple “ETM” (Element Transfer Method) (where the data on the new meshes are simply extrapolated based on the position of the new nodes/gauss points in the old mesh), we must first import it :
from wrap.mtDataTransfer import ETMCell
and then the command simply becomes :
autoRemesh.setInteractionToTransfer(no, ETMCell)
==== Changing the options ====
The FVTM transfer method has quite a few options and parameters which can be tuned by the aware user. This is simply done with the command addOption(optionType, optionChoice). For example :
from wrap.mtDataTransfer import *
#Data Transfer Properties
cell = autoRemesh.setInteractionToTransfer(no, FVTMCell)
cell.addOption(FVCELLTYPE, LINEARRECCELL)
cell.addOption(STENCILTYPE, LEASTSQUARE_STENCIL)
cell.addOption(LIMITERTYPE, SIMPLE_LIMITER)
cell.addOption(INTPT_NB, 5)
To understand all these options, please look at Philippe's doc.
==== Changing the fields to transfer ====
The list of fields which must be transferred is defined by default. If, among these fields, some are not to be transferred, this can be mentioned with the command addFieldToIgnore(field). For example :
autoRemesh = AutomaticRemeshing(getMetafor, file)
#Data Transfer Properties
cell = autoRemesh.setInteractionToTransfer(no, FVTMCell)
cell.addFieldToIgnore(IF_GRAIN_SIZE)
cell.addFieldToIgnore(IF_FTOTAL)
where IF_GRAIN_SIZE and IF_FTOTAL are the fields we do not wish to transfer.
==== Post-remeshing operations ====
After remeshing, all contact properties are lost. Therefore, we need to recompute the penetration of surface nodes into the contacts tools, redefine the corresponding forces, estimate the sticking or sliding state in the case of frictional contact and so on. All the interactions on which this must be done (typically, all contact interactions) are indicated with the command setInteractionToPostStep(no), where no is the user number of the interaction :
autoRemesh = AutomaticRemeshing(getMetafor, file)
autoRemesh.setInteractionToPostStep(101)
autoRemesh.setInteractionToPostStep(102)
will recompute all contact properties on the interaction 101 and 102.
===== Balancing =====
==== Introduction ====
After remeshing, the newly defined configuration is not in equilibrium due to :
* Geometrical errors in the interpolation of the new geometry.
* Errors due to the data transfer procedure from the old to the new mesh.
* The loss of sticking or sliding state of the nodes in contact.
Restarting the simulation from such a configuration can be tedious or even sometimes impossible. The balancing operations is therefore an additional step taking place after the transfer of data and before the restart of the temporal integration, aiming at restoring the equilibrium to allow a more efficient and accurate restart.
==== Example ====
When the boundary of the workpiece deformed by curved tools is remeshed, some nodes may exhibit large penetrations into the forming tools.
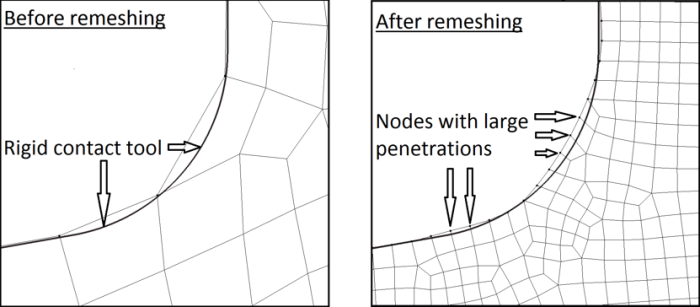 Since contact is enforced thanks to a penalty method, such spurious penetrations induce significant artificial retraction forces. When trying to restart the computation from such an unbalanced configuration, these forces can prevent the simulation from starting again.
Since contact is enforced thanks to a penalty method, such spurious penetrations induce significant artificial retraction forces. When trying to restart the computation from such an unbalanced configuration, these forces can prevent the simulation from starting again.
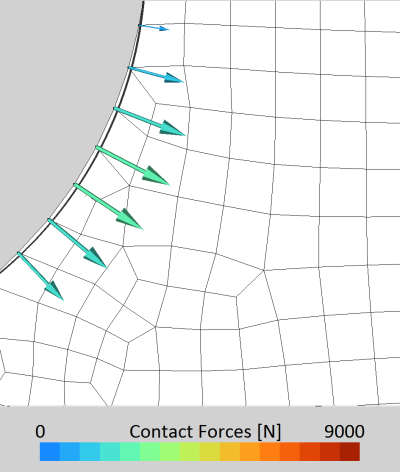
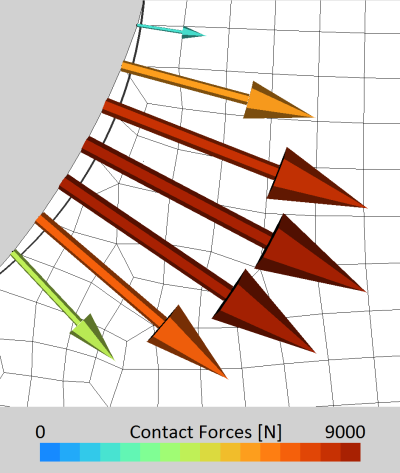 A post-remeshing balancing algorithm is then proposed in order to restore the equilibrium of the remeshed configuration. Before continuing the time integration, friction forces are recomputed, and corrections are made if the trace of the deviatoric stress tensor is non-zero. Afterwards, this post-remeshing algorithm progressively applies a fraction of the unbalanced forces as external forces, both for dynamic and quasi-static simulations. This brings back the nodes that penetrated too deeply into contact tools close to the boundary, and adjusts the positions of internal nodes of the mesh until equilibrium is reached. From this equilibrated configuration, the restart procedure can be conducted more efficiently.
A post-remeshing balancing algorithm is then proposed in order to restore the equilibrium of the remeshed configuration. Before continuing the time integration, friction forces are recomputed, and corrections are made if the trace of the deviatoric stress tensor is non-zero. Afterwards, this post-remeshing algorithm progressively applies a fraction of the unbalanced forces as external forces, both for dynamic and quasi-static simulations. This brings back the nodes that penetrated too deeply into contact tools close to the boundary, and adjusts the positions of internal nodes of the mesh until equilibrium is reached. From this equilibrated configuration, the restart procedure can be conducted more efficiently.
 ==== Quasi-static balancing====
The equation which must be verified for each time step of a quasi-static integration is simply
$\boldsymbol{F}^{int}=\boldsymbol{F}^{ext}$
After remeshing and data transfer, this equation is no longer true, so we have (where the index $t$ in $\boldsymbol{F}_t$ means that we consider the value after transfer)
$\boldsymbol{F}^{unbal} = \boldsymbol{F}^{int}_t - \boldsymbol{F}^{ext}_t$
The post-remeshing algorithm is simply a variation of the quasi-static integration scheme where this imbalance is to be solved. First, we simply try to solve the equation as it is. If it works, then the imbalance is corrected and the real integration can start again. If it does not work, then an increasing fraction of the unbalanced forces are applied as external forces, in order to solve the imbalance little by little. Once verified for a given fraction, the the unbalanced forces are recomputed and the algorithm started again, until equilibrium is restored.
Mathematically, we are therefore trying to solve for $\boldsymbol{F}^{int}$ the equation :
$\boldsymbol{F}^{int}=\boldsymbol{F}^{ext}_t + (1-\alpha) \boldsymbol{F}^{unbal} = \boldsymbol{F}^{ext}_t + (1-\alpha) (\boldsymbol{F}^{int}_t - \boldsymbol{F}^{ext}_t)$
where $\alpha$ is first equal to one, then if progressively divided by two as long as the equation cannot be solved
(when $\alpha$ tends to one, we see indeed that the equation is trivially verified).
==== Dynamic balancing====
In the case of a simulation using an Alpha-Generalised integration scheme, we try to solve the equation
$$(1-\alpha_M) \boldsymbol{F}^{\text{inert}}(t^{n+1}) + \alpha_M \boldsymbol{F}^{\text{inert}}(t^n) + (1-\alpha_F) \boldsymbol{F}^{\text{int}}(t^{n+1}) + \alpha_F \boldsymbol{F}^{\text{int}}(t^n)$$
$$ = (1-\alpha_F) \boldsymbol{F}^{\text{ext}}(t^{n+1}) + \alpha_F \boldsymbol{F}^{\text{ext}}(t^n)$$
The idea is similar : after remeshing, there is some imbalance and the equation is no longer verified, so we want to apply a balancing algorithm to restore equilibrium before restarting the computation. Since the time is stopped, inertial forces are kept as they are and only internal forces are modified to satisfy equilibrium. In the same way as for a quasi-static simulation, this is done by applying as external forces an increasing fraction of the unbalanced forces. The difference with respect to the quasi-static algorithm is the expression of the unbalanced forces, which will here also contains the inertial forces and the forces computed at the previous time step.
Since we conserve the inertial forces and correct the internal ones, this post-remeshing algorithm works quite well for quasi-static and low speed dynamic computations. For high speed dynamic computations, it is best not to use it and simply let the simulation continue.
==== Options ====
The complete
==== Quasi-static balancing====
The equation which must be verified for each time step of a quasi-static integration is simply
$\boldsymbol{F}^{int}=\boldsymbol{F}^{ext}$
After remeshing and data transfer, this equation is no longer true, so we have (where the index $t$ in $\boldsymbol{F}_t$ means that we consider the value after transfer)
$\boldsymbol{F}^{unbal} = \boldsymbol{F}^{int}_t - \boldsymbol{F}^{ext}_t$
The post-remeshing algorithm is simply a variation of the quasi-static integration scheme where this imbalance is to be solved. First, we simply try to solve the equation as it is. If it works, then the imbalance is corrected and the real integration can start again. If it does not work, then an increasing fraction of the unbalanced forces are applied as external forces, in order to solve the imbalance little by little. Once verified for a given fraction, the the unbalanced forces are recomputed and the algorithm started again, until equilibrium is restored.
Mathematically, we are therefore trying to solve for $\boldsymbol{F}^{int}$ the equation :
$\boldsymbol{F}^{int}=\boldsymbol{F}^{ext}_t + (1-\alpha) \boldsymbol{F}^{unbal} = \boldsymbol{F}^{ext}_t + (1-\alpha) (\boldsymbol{F}^{int}_t - \boldsymbol{F}^{ext}_t)$
where $\alpha$ is first equal to one, then if progressively divided by two as long as the equation cannot be solved
(when $\alpha$ tends to one, we see indeed that the equation is trivially verified).
==== Dynamic balancing====
In the case of a simulation using an Alpha-Generalised integration scheme, we try to solve the equation
$$(1-\alpha_M) \boldsymbol{F}^{\text{inert}}(t^{n+1}) + \alpha_M \boldsymbol{F}^{\text{inert}}(t^n) + (1-\alpha_F) \boldsymbol{F}^{\text{int}}(t^{n+1}) + \alpha_F \boldsymbol{F}^{\text{int}}(t^n)$$
$$ = (1-\alpha_F) \boldsymbol{F}^{\text{ext}}(t^{n+1}) + \alpha_F \boldsymbol{F}^{\text{ext}}(t^n)$$
The idea is similar : after remeshing, there is some imbalance and the equation is no longer verified, so we want to apply a balancing algorithm to restore equilibrium before restarting the computation. Since the time is stopped, inertial forces are kept as they are and only internal forces are modified to satisfy equilibrium. In the same way as for a quasi-static simulation, this is done by applying as external forces an increasing fraction of the unbalanced forces. The difference with respect to the quasi-static algorithm is the expression of the unbalanced forces, which will here also contains the inertial forces and the forces computed at the previous time step.
Since we conserve the inertial forces and correct the internal ones, this post-remeshing algorithm works quite well for quasi-static and low speed dynamic computations. For high speed dynamic computations, it is best not to use it and simply let the simulation continue.
==== Options ====
The complete setBalancing command is actually
setBalancing(executeBalancing, velocitiesExtrapolation=True, maxItes=7, balancingTolerance=0.001)
The first argument has already been described and indicates whether balancing should be done or not.
For the advanced user, a few options can be played with by changing the three of arguments.
First of all, it is possible to deactivate the stepPredictor(). If you do not know what it is, do not touch it. If you do, well sometimes, when transfer errors are significant, the balancing can go better if executed without this predictor, so without extrapolating the next step based on velocities and accelerations. This is fine only in quasi-static, because in dynamic computations velocities and accelerations also intervene in the computation of forces. To do so, simply set the second argument to False. If have not investigated this greatly, but I believe that this could be a sign that the mesh of the computation was not fine enough, so activating this option could hide the real problem. I believe it should be reserved for battery tests, because we want to have tests with rather coarse meshes there.
Second, the number of iterations for each step of the balancing can be changed. By default, seven iterations are tried before increasing the fraction of the unbalanced forces and starting again.
Finally, the tolerance can also be changed. The parameter $\alpha$, used to ponder the unbalanced forces, starts at 1 and is progressively divided by 2 when a step fails. Once $\alpha$ becomes smaller than the tolerance, the algo stops itself, returns an error, and the temporal integrationdoes not restart. The default value of 0.001 can be changed if needed.
— Pierre Joris 2016/06/13