This is an old revision of the document!
Table of Contents
Curves
Introduction
- A curve orientation is given by the succession if its points. For example, a straight line is oriented from its first point towards its second point. This orientation is relevant when defining contact matrices, for instance. For 2D rigid-deformable contact, a curve must be defined with “area to the left”, which means that the normal must point towards the inside of the matter (also applicable with
Surfacesin 3D). - The normal of a curve is defined such as $\boldsymbol{t} \wedge \boldsymbol{n} = (0,0,1)$.
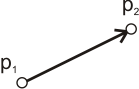
Line: Straight Segment
A Line (line segment) is defined with its two vertices.
line = curveset.add( Line(number, pt1, pt2) )
with
number | user number (unique among Curves and $\ge 1$) |
pt1,pt2 | the 2 Points used as vertices |
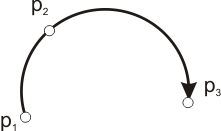
Arc: Arc of Circle
An Arc of circle is defined using three points, as shown on the figure.
arc = curveset.add( Arc(number, pt1, pt2, pt3) )
with
number | user number (unique among Curves and $\ge 1$) |
pt1,pt2,pt3 | the 3 Points |
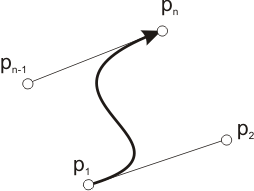
Cubic Spline
"Open" Cubic Spline
spl = curveset.add( CubicSpline(number, [pt1, pt2, pt3, pt4]) )
spl.useLsTangent() # tangents are calculated
# using local reconstruction [DEFAULT]
spl.useLittTangents() # tangents are calculated
# using Litt/Beckers lectures
with
number | user number (unique among Curves and $\ge 1$) |
pt1,pt2,pt3,… | the list of Points |
"Closed" Cubic Spline
To close a spline, the first and last points of the list must be the same.
spl = CubicSpline(number, [pt1, pt2, pt3, pt4, ..., pt1])
Spline-reconstruction based on a mesh
![]() It is possible to construct a spline based on the mesh of a line. This way, a smooth approximation of this mesh if obtained.
It is possible to construct a spline based on the mesh of a line. This way, a smooth approximation of this mesh if obtained.
spl = CubicSpline(number, obj)
where obj is a meshed object.
Circle: Full Circle
A circle is defined with its center and radius (this function is only defined in the $z=0$ plane)
circ2d = curset.add( Circle(number, centre, R) )
with
number | user number (unique among Curves and $\ge 1$) |
centre | centre Point |
R | radius |
The orientation of the Circle can be inverted (and so will its tangent and normal used for contact):
circ2d.reverse()
NURBS
A Non-Uniform Rational Basis Spline (N.U.R.B.S.) is defined as:
nur = curset.add( NurbsCurve(number) ) nur.setDegree(degree) nur.push(pt1); nur.pushWeight(weight1) nur.push(pt2); nur.pushWeight(weight2) nur.pushKnot(knot1) nur.pushKnot(knot2)
where
number | user number (unique among Curves and $\ge 1$) |
pt1, pt2 | Points used as supports |
degree | degré de la coube |
weight1, weight2 | weights |
knot1, knot2 | knot vector |
PythonCurve: Python-interpreted Curves
If a Curve is not implemented in Metafor, it can be programmed in python using the generic Curve called PythonCurve.
The method .push() is used to add points.
PythonCurve possesses four member functions that can be overloaded. The method named setEval(fct) is used to defined the evaluation python function. The methods named setTg, setDTg andsetLen() respectively define the tangent, its derivative and the curvilinear abscissa. The function setEval(fct) is the only one required to mesh the curve, when the other three are used for contact.
Example:
See toolbox.curves which defines a Parabola. The input file apps.qs.parabola is an example of application.
from toolbox.curves import Parabola parab = curset.add(Parabola(1, pt1, pt6, pt2))
These lines create a parabola #1, based on the three previously defined points pt1, pt6 and pt2.