Table of Contents
2D Meshers (Surfaces)
Metafor has a few integrated meshers, quite simple but usually capable of meshing parts that are not too complicated. However, 2D meshers require that the wire delimiting the domain has the right orientation. The wire must be defined with its “area to the left”, which means that when the wire is followed along its orientation (defined by the succession of its curves), the matter of the part is on the left-hand
Transfinite mesher
With auto-detection
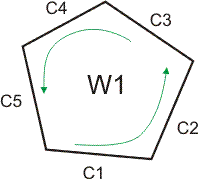
The auto-detection is working if the Sides is made of 4 edges, each of which is only made of one Curve.
TransfiniteMesher2D(sideset(number)).execute(type, tri)
number | = number of the Side to mesh |
type | = True if mesh elements must be generated = False if only nodes must be generated (useful in 3D!) |
tri | = 0 to generate quads (CELL_QUAD) [default] = 1 to generate triangles from the first node (CELL_TRIANGLE) = 2 to generate triangles from the second node (CELL_TRIANGLE) |
In the example above, the auto-detection is doable.
A similar function for higher degrees is:
HighDegreeTransfiniteMesher2D(sideset(number), degree).execute(type, sideNode, tri)
number | = number of the side Side |
degree | = mesh degree (2 or 3) |
type | = True if mesh elements must be generated = False if only nodes must be generated (useful in 3D!) |
sideNode | = True to generate 9-nodes mesh elements (CELL_NINE_QUADRATIC_QUAD) = False to generate 8-nodes mesh elements (CELL_QUADRATIC_QUAD) |
tri | = 0 to generate quads (CELL_QUAD) [default] = 1 to generate triangles from the first node (CELL_TRIANGLE) = 2 to generate triangles from the second node (CELL_TRIANGLE) |
For 9-nodes mesh elements, the central node is linked to the Side.
For 16-nodes mesh elements, central nodes are linked to the Side.
Without auto-detection
mat = ((mat11, mat12, ..., mat1nbmax),
(mat21, mat22, ..., mat2nbmax),
(mat31, mat32, ..., mat3nbmax),
(mat41, mat42, ..., mat4nbmax) )
TransfiniteMesher2D(sideset(number)).execute2(mat, type, tri)
where mat is a python tuple with 4 components. Each component is a tuple which contains the number of the curves which constitute each edge. Each of these four edges can be made of a different number of curves.
Example:
This face can be meshed by the command:
TransfiniteMesher2D(sideset(1)).execute2( (1,2,(3,4),5) )
The order of the lines does not matter in 2D (in opposition to the 3D case). Therefore, the following command also works:
TransfiniteMesher2D(sideset(1)).execute2( ((4,3),1,2,5) )
Transfinite mesher on a side
The mesh can be projected on the surface surfNo (whether with or without auto-detection) if this surface is associated to the Side before the meshing operation:
sideset(1).setSurfaceNo(surfNo)
2D transfinite mesher with a non-uniform mesh elements distribution
This is done with the commands:
MesherTFI2D =TransfiniteMesher2D(sideset(number)) MesherTFI2D.setEnableDistribution() MesherTFI2D.execute(type, tri) or MesherTFI2D.execute2(mat, type)
when one if the edges is already discretized using a mesh elements distribution.
Note : By default, the parameter of the function setEnableDistribution is set to True.
Frontal mesher
Description
This mesher is a new implementation of L. Stainer's work, which contains an offset and frontal mesher. It is usually rather disappointing.
Use
Triangles (frontal):
sidset(no).frontalTriangle(d)
Quadrangles (offset + frontal):
sidset(no).frontalQuad(d)
where d is the average length of the mesh elements edges to generate.
Gen4 mesher
Description
This quadrangular mesher is based on Sarrate algorithm. This method consists in diving the domain in a recursive way until only one quadrangle remains. It is very robust, and enables efficient meshing of complex domains.
Possibilities
Gen4 can be used to mesh:
- any planar face (convex or not, with or without holes)
- including density (linear interpolation between two values specified on the vertices of the face).
- including the “background mesh” type (density specified on a secondary mesh).
- with integrated smoothing
- with topological correction
Use
These lines are used to mesh the face #1 of the domain, whose vertices (points #1, #2, #3 and #4) densities are 0.1, 0.1, 0.2 and 0.05.
from toolbox.meshers import Gen4Mesher defaultDensity = 0.1 mesher = Gen4Mesher(sideset(1), domain, defaultDensity) mesher.setPointD(3,0.2) mesher.setPointD(4,0.05) mesher.execute()
A default density, used unless explicitly stated differently, can be defined. This way, a density is only defined on specific mesh points. If no value is assigned in the data set, $0.1$ is taken as default density value.
CAREFUL : The face #1 must be defined in the XY plane.
Triangular mesher
Description
Create triangles on a planar face, as a function of
- the maximal area of the triangle
- the maximal angle of the triangle
Use
See, for example, the case apps.qs.triangleMesher. After creating a face Side(1), it was meshed with a maximal area of 0.05 as criterion.
from toolbox.meshers import TriangleMesher mesher = TriangleMesher(sideset(1), domain) #mesher.setMaxAngle(20) mesher.setMaxArea(0.05) mesher.execute()
