Table of Contents
Functions y=f(t)
Functions are quite useful to describe how some parameters evolve, over time for example. They can be used to prescribe displacements or to define hardening laws.
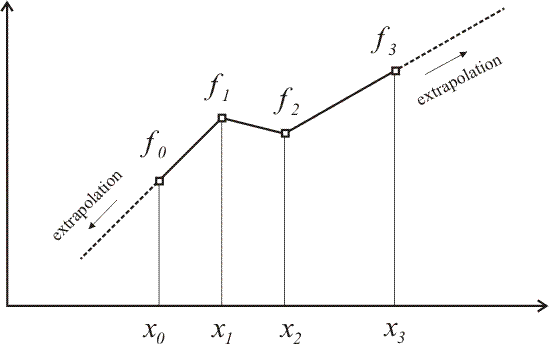
PieceWiseLinearFunction
A piecewise linear function is defined one point at a time:
fct = PieceWiseLinearFunction() fct.setData(abs1, ord1) fct.setData(abs2, ord2) ...
where
abs1, abs2, … | list of abscissae |
ord1, ord2, … | list of ordinates |
Remark: As can be seen above, the first and last segments are extrapolated if a value of the function is required outside its domain.
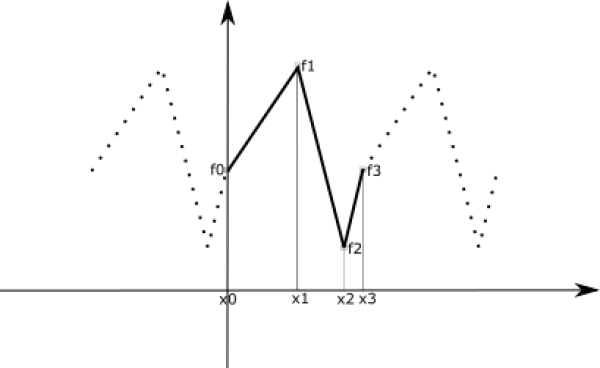
CyclicPieceWiseLinearFunction
The CyclicPieceWiseLinearFunction allows to duplicate infinitely a PieceWiseLinearFunction.
2 constrains are applied on Data :
- the first abcisse must be equal to 0.0 (abs1 = 0.0)
- the cycle must be closed (ord1 = ordLast)
PythonOneParameterFunction
If a function is mathematically too complex to be defined with a PieceWiseLinearFunction, it can be defined analytically, with a PythonOneParameterFunction object.
def f(x):
[function calculating y=f(x)]
return y
fct1 = PythonOneParameterFunction(f)
For example, this is used to:
- Set the node density for a 1D mesher (1D Meshers (Curves)).
- define elaborated prescribed displacements (Prescribed Displacements).
- Define a hardening function with Python (General Points).
Examples
The ramp function:
fct1 = PieceWiseLinearFunction() fct1.setData(0,0) fct1.setData(1,1)
can be also defined with a classical python function:
def f(x):
return x
fct1 = PythonOneParameterFunction(f)
or, using python lambda function:
f = lambda x: x fct1 = PythonOneParameterFunction(f)
Advanced use
![]() The value can also be displayed for each estimation, and a more complex function can also be defined using all Python tools. For example, a load function can be first defined with a parabola, then with a straight line, the change between these two being controlled by an conditional structure.
The value can also be displayed for each estimation, and a more complex function can also be defined using all Python tools. For example, a load function can be first defined with a parabola, then with a straight line, the change between these two being controlled by an conditional structure.
def f(a):
val=0
if(a‹0.5):
val=a*a
else:
x=0.5*0.5;
val=x+(a-0.5)/(1-0.5)*(1-x)
print 'value=', val
return val
fct1 = PythonOneParameterFunction(f)