Table of Contents
Commit 2017-08-16
Ce commit est pour améliorer quelques routines liées au contact et pour mettre progressivement mes développements sur la version courante.
Cas Test - Schéma d'augmentation alternative
Afin de conserver une trace de l'interface des nouvelles méthodologies, j'ai ajouté les cas tests implémentés et présentés lors de la conférence ICCCM 2017.
Boundary Volume Hierarchy
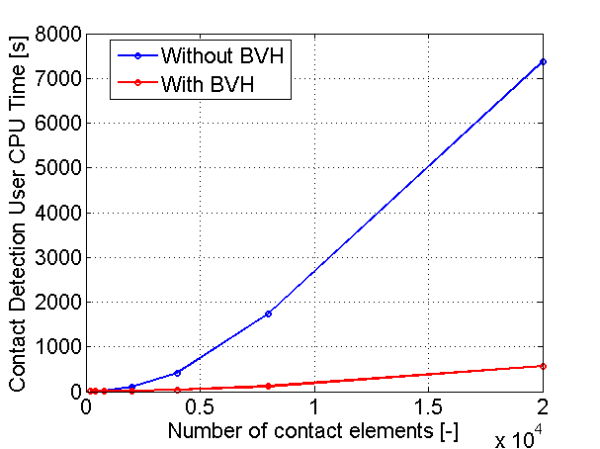
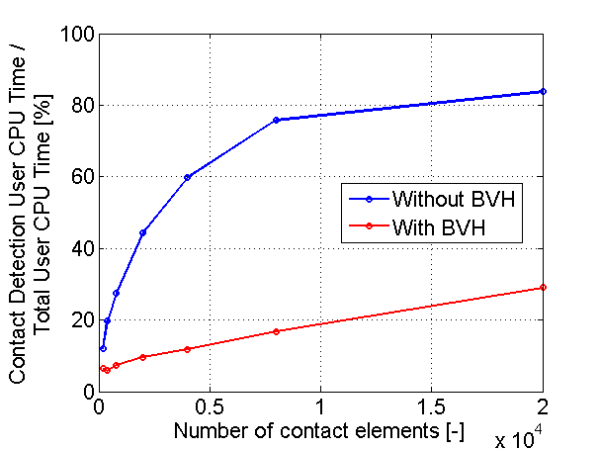
La détection du contact dans Metafor peut être séparée en deux phases distinctes : détection globale et détection locale. La détection globale indique grossièrement sur quelle portion de l'entité maître le nœud esclave sera potentiellement en contact tandis que la détection locale détermine la projection du nœud esclave sur cette portion de l'entité maître. La phase de détection globale se fait en général à l'aide de boites alignées selon les axes Cartésiens et elle est critique dans le cas du contact entre corps déformable. En effet, dans ce cas là, nous devons parcourir l'ensemble des facettes du corps maître et répertorier toutes les projections valides avant décider laquelle d'entre elles sera la bonne projection. Dans ce cas là, on constate que le temps de calcul peut littéralement exploser si on augmente le nombre d'éléments sur la surface du corps maître, car on a une tendance du type O(N*M) avec N = le nombre de facettes du corps maître et M = le nombre de nœuds du corps esclave.
Pour améliorer l'efficacité de l'algorithme de détection du contact, un algorithme de recherche sous forme d'arbre binaire a été implémenté dans Metafor. Cet algorithme permet de récupérer aisément les facettes sur laquelle nous devons effectuer la détection locale.
Je vous fournis aussi les références utilisées pour l'implémentation :
- Bin Yang, Tod A. Laursen : A contact searching algorithm including bounding volume trees applied to finite sliding mortar formulations [2006]
- T. L. Kay & J. T. Kajiya, Ray tracing complex scenes [1986] (Spatial median splits)
- Efficient Collision Detection Using Bounding Volume Hierarchies of k-DOPs, J. T. Klosowski et al. [1998] (k-DOPs)
Par exemple, le cas de l'impact entre deux anneaux.
Détails d'implémentation
Les routines de manipulation sur les nœuds de l'arbre se fait au moyen d'un appel à fonction récursif au lieu de l'utilisation d'une queue.
L'arbre se trouve sous forme d'un std::vector organisé d'un manière telle que les nœuds gauche et droite sont directement contigus.
La construction de l'arbre se fait au moyen d'une approche dite top-down. A partir du centre géométrique des objets, on définit un plan de partitionnement à partir duquel on sépare les objets de part et d'autre de ce plan pour former les nœuds intérieurs gauche et droite de l'arbre. On procède récursivement jusqu'à ce que nous n'ayons plus que deux objets à partitionner.
Chaque nœud de l'arbre possède un volume d'approximation (Bounding Volume), ce qui permet aisément de mettre à jour tous les volumes d'approximation à partir des feuilles de l'arbre vers la racine de l'arbre (Approche bottom-up), puisque les feuilles contiennent les entités géométriques. Au niveau des feuilles de l'arbre, on a le calcul d'un volume d'approximation et ensuite on a une union des volumes d'approximation pour les volumes pour les nœuds intermédiaires.
Finalement, les classes liées à la gestion d'un arbre des volumes d'approximation ont été implémentées sous forme de template.
Cas Test
Le système de recherche sous forme d'arbre s'active par la commande suivante :
ci1 = RdContactInteraction(1) ci1.push(wireset(1)) ci1.setTool(wireset(2)) ci1.setUseBVH(parameters['useBVH']) parameters['useBVH'] = True | False interactionset.add(ci1)
Je vous indique ici les différentes performances observées avec quelques cas-tests de la batterie :
| Cas test | CPU sans BVH (sec) | CPU avec BVH (sec) | Différence (sec) |
| apps.imp.ddrawingBVH | 169.672 | 168.859 | 0.813 (0.5 %) |
| meca0464.tests.threeRingsContactTest | 36.6406 | 28.2344 | 8.4062 (23 %) |
| meca0464.tests.twoRingsContactTest | 12.6406 | 11.9375 | 0.703 (5.5 %) |
| mtContact.tests.threePlatesCylinderContactTest | 922.141 | 558.453 | 363.688 (39 %) |
| mtContact.tests.threeBeamsRingContactTest | 332.547 | 182.609 | 149.938 (45 %) |
| mtContact.tests.torusCylinderContactTest | 622.391 | 329.219 | 293.172 (47 %) |
| mtContact.tests.twoToriContactTest | 251.141 | 173.453 | 77.688 (31 %) |
Finalement, il est très recommandé d'utiliser cet algorithme d'arbre lors d'un cas test de contact en défo-défo.
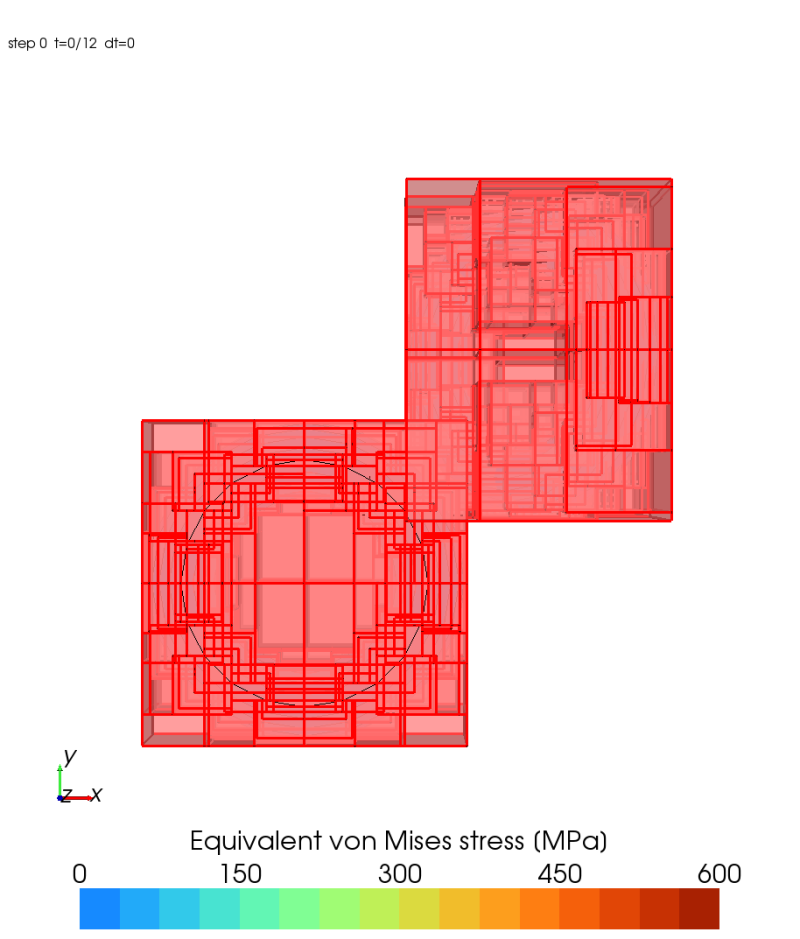
Visualisation Graphique
J'ai ajouté la possibilité de voir les arbres dans Metafor. Je vous fournis ici quelques captures d'écran :
Extensions possibles
Il y a trois aspects sur lesquels on peut encore améliorer la recherche sous forme d'arbre pour la détection globale :
- Parcourir/Mettre à jour l'arbre à l'aide d'une boucle parallélisée en utilisant l'outil TBB : pour se faire, il faudra surement réécrire la routine à l'aide d'une queue pour facilement pouvoir paralléliser;
- Utiliser des volumes d'approximation d'un ordre supérieur à la boite (k-DOP);
- Mettre à jour l'arbre sous forme de rotation/déplacement rigide dès que possible (pour le contact rigide déformable permettra de gagner du temps, car les boites seront calculées uniquement lors de la phase d'initialisation et déplacer ensuite par l'intermédiaire cette transformation géométrique). Ceci est facilement conceptuellement mais délicat à implémenter proprement dans Metafor.
Finalement, une autre manière d'accélérer le calcul des projections dans le cas de surface ou courbe de type NURBS est de proposer une approximation de la surface/la courbe à l'aide d'une triangularisation/segmentation et de construire un arbre sur cette approximation pour procéder aux calculs des projections.
Intégration numérique
Afin de calculer une surface, une longueur, ainsi qu'un centre de gravité aisément, j'ai implémenté une quadrature automatique du type Clenshaw-Curtis (Stratégie de sous-division locale). Également afin de conserver une certaine généralité, j'ai proposé une version templatisée de cet intégrateur. L'intégrateur fonctionne pour des intégrants scalaires, vectorielles et des domaines d'intégration 1D, 2D et 3D.
Références :
- Computational Integration de Arnold R. Krommer et Christoph W. Ueberhuber, p 427
- A self-adaptive Clenshaw-Curtis quadrature scheme for efficient integration over parametric CAD surfaces, R.N. Simpson, Z. Liu, University of Glasgow
- Is Gauss quadrature better than Clenshaw-Curtis ?, Lloyd N. Trefethen, 2008
Fichiers ajoutés/supprimés
[a]:oo_meta\mtDrawables\BVHTreeDrawer.cpp [a]:oo_meta\mtDrawables\BVHTreeDrawer.h [a]:oo_meta\mtGeo\mtGeoBoundaryVolume.cpp [a]:oo_meta\mtGeo\mtGeoBoundaryVolume.h [a]:oo_meta\mtGeo\mtGeoBoundaryVolumeHierarchy.cpp [a]:oo_meta\mtGeo\mtGeoBoundaryVolumeHierarchy.h [a]:oo_meta\mtGeo\mtGeoBoundaryVolumeHierarchyTemplate.cpp [a]:oo_meta\mtGeo\mtGeoBoundaryVolumeHierarchyTemplate.h [a]:oo_meta\mtGeo\mtGeoBoundaryVolumeHierarchyTemplate.hpp [a]:oo_meta\mtGeo\mtGeoBVHBuilder.cpp [a]:oo_meta\mtGeo\mtGeoBVHBuilder.h [a]:oo_meta\mtGeo\mtGeoBVHTreeNode.cpp [a]:oo_meta\mtGeo\mtGeoBVHTreeNode.h [a]:oo_meta\mtGeo\mtGeoBVHType.h [a]:oo_meta\mtGeo\mtGeoCurveIntegrands.cpp [a]:oo_meta\mtGeo\mtGeoCurveIntegrands.h [a]:oo_meta\mtGeo\mtGeoGObjectIntegrandTemplate.h [a]:oo_meta\mtGeo\mtGeoGObjectIntegrandTemplate.inl [a]:oo_meta\mtGeo\mtGeoSelfBVHTreeNode.cpp [a]:oo_meta\mtGeo\mtGeoSelfBVHTreeNode.h [a]:oo_meta\mtGeo\mtGeoSelfTopDownBVHBuilder.cpp [a]:oo_meta\mtGeo\mtGeoSelfTopDownBVHBuilder.h [a]:oo_meta\mtGeo\mtGeoSurfaceIntegrands.cpp [a]:oo_meta\mtGeo\mtGeoSurfaceIntegrands.h [a]:oo_meta\mtGeo\mtGeoTopDownBVHBuilderTemplate.h [a]:oo_meta\mtGeo\mtGeoTopDownBVHBuilderTemplate.hpp [a]:oo_meta\mtGeo\mtGeoWithBoundaryVolume.cpp [a]:oo_meta\mtGeo\mtGeoWithBoundaryVolume.h [a]:oo_meta\mtGeo\mtGeoWithBoundaryVolumeTemplate.cpp [a]:oo_meta\mtGeo\mtGeoWithBoundaryVolumeTemplate.h [a]:oo_meta\mtGeo\mtGeoWithBoundaryVolumeTemplate.hpp [a]:oo_meta\mtMath\AdaptiveClenshawCurtisIntegrators.cpp [a]:oo_meta\mtMath\AdaptiveClenshawCurtisIntegrators.h [a]:oo_meta\mtMath\AdaptiveClenshawCurtisIntegratorTemplate.h [a]:oo_meta\mtMath\AdaptiveClenshawCurtisIntegratorTemplate.inl [a]:oo_meta\mtMath\ClenshawCurtisQuadratureRule.cpp [a]:oo_meta\mtMath\ClenshawCurtisQuadratureRule.h [a]:oo_meta\mtMath\ClenshawCurtisQuadratureRule.inl [a]:oo_meta\mtMath\ClenshawCurtisTestSuiteChecker.cpp [a]:oo_meta\mtMath\ClenshawCurtisTestSuiteChecker.h [a]:oo_meta\mtMath\Integrands.cpp [a]:oo_meta\mtMath\Integrands.h [a]:oo_meta\mtMath\IntegrandTemplate.h [a]:oo_meta\mtMath\IntegrandTemplate.inl [a]:oo_meta\mtMath\IntegrationDomains.cpp [a]:oo_meta\mtMath\IntegrationDomains.h [a]:oo_meta\mtMath\IntegrationDomainTemplate.h [a]:oo_meta\mtMath\IntegrationDomainTemplate.inl [r]:
Cas tests ajoutés/supprimés
[a]:oo_nda/meca0464/tests/threeRingsContactTestBVH.py [a]:oo_nda/meca0464/tests/twoRingsContactTestBVH.py [a]:oo_meta\apps\imp\ddrawingBVH.py [a]:oo_meta\mtContact\tests\cylindricalIndentation.py [a]:oo_meta\mtContact\tests\cylindricalIndentationBarzilaiBorwein.py [a]:oo_meta\mtContact\tests\cylindricalIndentationExtrapolation.py [a]:oo_meta\mtContact\tests\cylindricalIndentationNesterov.py [a]:oo_meta\mtContact\tests\cylindricalIndentationUzawa.py [a]:oo_meta\mtContact\tests\deepDrawing.py [a]:oo_meta\mtContact\tests\deepDrawingBarzilaiBorwein.py [a]:oo_meta\mtContact\tests\deepDrawingExtrapolation.py [a]:oo_meta\mtContact\tests\deepDrawingNesterov.py [a]:oo_meta\mtContact\tests\deepDrawingUzawa.py [a]:oo_meta\mtContact\tests\slidingElasticBlock.py [a]:oo_meta\mtContact\tests\slidingElasticBlockBarzilaiBorwein.py [a]:oo_meta\mtContact\tests\slidingElasticBlockBarzilaiBorweinLimit20.py [a]:oo_meta\mtContact\tests\slidingElasticBlockBarzilaiBorweinLimit5.py [a]:oo_meta\mtContact\tests\slidingElasticBlockBarzilaiBorweinNoLimit.py [a]:oo_meta\mtContact\tests\slidingElasticBlockBarzilaiBorweinNoStability.py [a]:oo_meta\mtContact\tests\slidingElasticBlockBarzilaiBorweinNoStabilityNoLimit.py [a]:oo_meta\mtContact\tests\slidingElasticBlockExtrapolationNoStability.py [a]:oo_meta\mtContact\tests\slidingElasticBlockExtrapolationNoStabilityNoLimit.py [a]:oo_meta\mtContact\tests\slidingElasticBlockNesterov.py [a]:oo_meta\mtContact\tests\slidingElasticBlockUzawa.py [a]:oo_meta\mtContact\tests\slidingElasticExtrapolation.py [a]:oo_meta\mtContact\tests\slidingElasticExtrapolationLimit075.py [a]:oo_meta\mtContact\tests\slidingElasticExtrapolationLimit3.py [a]:oo_meta\mtContact\tests\slidingElasticExtrapolationNoLimit.py [a]:oo_meta\mtContact\tests\slidingElasticNesterovNoStability.py [a]:oo_meta\mtContact\tests\threeBeamsRingContactTestBVH.py [a]:oo_meta\mtContact\tests\threePlatesCylinderContactTestBVH.py [a]:oo_meta\mtContact\tests\torusCylinderContactTestBVH.py [a]:oo_meta\mtContact\tests\twoToriContactTestBVH.py [a]:oo_meta\mtMath\tests\adaptiveClenshawCurtisIntegrators.py [r]:
— gaëtan 2017/08/16 12:00