En marge de nos essais de simulations numériques du banc SNECMA du blisk, le besoin d'affûter nos réglages d'amortissement dans un cadre dynamique vibratoire (intégrateur dynamique implicite $\alpha$-généralisé Chung-Hulbert) est devenu primordial pour pouvoir espérer reproduire les résultats recherchés.

Pour calibrer nos paramètres d'amortissement, nous procédons à des analyses paramétriques avec un cas-test spécifiquement mis au point : le calcul de la réponse impulsionnelle d'une aube (voir Figure 1). Ce nouveau cas-test vient donc compléter la stratégie déjà établie avec notre modèle du banc 18ER pour préparer les simulations d'interaction aube/carter.

L'objectif affiché est de se faire une première idée précise des choix de paramètres contrôlant l'amortissement (taille du pas de temps $h$ et valeur asymptotique du rayon spectral $\rho_\infty$) avec un coût de calcul bas, avant même d'entamer des simulations d'interaction nettement plus coûteuses. En particulier, dans le cas du banc SNECMA du blisk qui nous occupe, il nous faut nous assurer que nous n'amortissons pas excessivement les modes d'intérêt 1F, 1T et 2F des aubes (modes relevés par expérience dans l'essai de SNECMA).

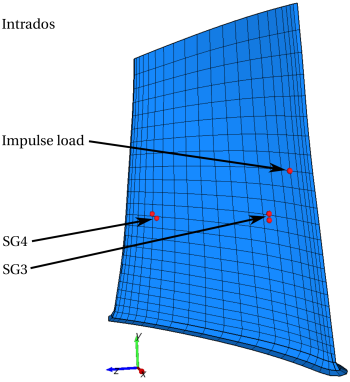Figure 1 : Application d'une impulsion sur une aube isolée du blisk.

D'après [1], une technique parmi d'autres pour calculer la réponse dynamique après une impulsion unitaire au degré de liberté $j$ au temps $t = 0$ est d'imposer une vitesse initiale selon l'expression suivante : \begin{equation} \boldsymbol{M} \boldsymbol{\dot{u}}_0 = \boldsymbol{1}_j \end{equation} où $\boldsymbol{\dot{u}}_0$ est le vecteur structural de vitesses nodales initiales, $\boldsymbol{M}$ est la matrice de masse et $\boldsymbol{1}_j$ est un vecteur avec un coefficient unitaire pour le degré de liberté $j$. Par conséquent, la réponse impulsionnelle peut se calculer en imposant une force externe nulle et commencer l'intégration temporelle avec l'ensemble de conditions initiales suivantes : \begin{align} \boldsymbol{u}_0 &= \boldsymbol{0} \label{eq:vo:1}\\ \boldsymbol{\dot{u}}_0 &= \boldsymbol{M}^{-1} \boldsymbol{1}_j \label{eq:vo:2}\\ \boldsymbol{\ddot{u}}_0 &= \boldsymbol{M}^{-1} \left( -\boldsymbol{C} \boldsymbol{\dot{u}}_0 \right) \label{eq:vo:3} \end{align}

Dans le code source, la classe des conditions initiales (InitialConditionSet) se voit dès à présent enrichie par la méthode defineImpulse(mtGeo::GObject &_target, Field1D &_comp, double _ampl) qui permet d'instancier un objet de type ImpulseUniformLoading. Cette nouvelle classe ImpulseUniformLoading comprend la méthode genericTotalUpdate(double t) qui permet d'appliquer une impulsion à partir d'une vitesse initiale $\boldsymbol{\dot{u}}_0$ selon l'équation ci-dessus.

De plus, il est à noter que l'utilisateur peut spécifier la valeur du coefficient pour le degré de liberté $j$ en argument de la méthode. Par défaut, sa valeur vaut l'unité.

Pour l'heure, il est aussi à noter que _target est une référence à une entité géométrique à un seul point uniquement. Dans le cas contraire, si l'entité géométrique ne comprend pas un seul point, une erreur fatale est déclenchée.

[1] D. J. RIXEN et P. L. van der VALK. « An Impulse Based Substructuring approach for impact analysis and load case simulations ». In : Journal of Sound and Vibration 332.26 (2013), p. 7174–7190. ISSN : 0022-460X, http://dx.doi.org/10.1016/j.jsv.2013.08.004

Dans notre modèle numérique du blisk (version NEWAC), nous avions un extracteur des 6 composantes du tenseur de déformation. Avec cet extracteur, nous calculions une valeur moyenne des valeurs extrapolées aux 4 noeuds d'une face d'un élément fini (voir Figure 2). Dans le post-traitement Matlab, les signaux de jauges étaient calculés à partir de ces 6 composantes du tenseur de déformation et d'une matrice de rotation qui permettait de prendre en compte l'orientation de la jauge dans le plan de l'aube et l'angle polaire de l'aube.

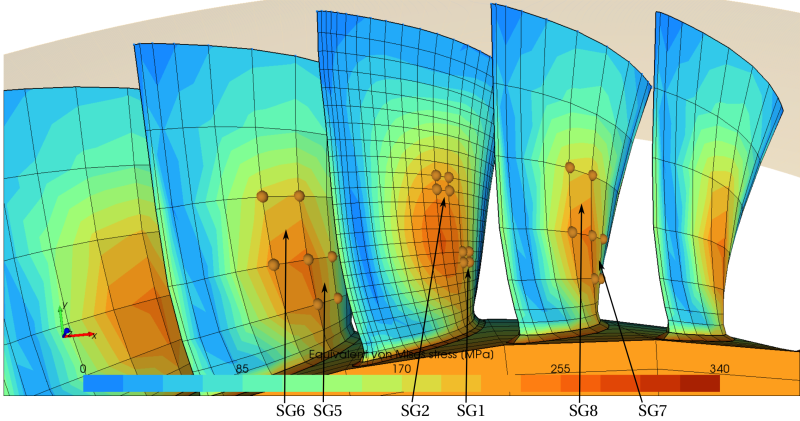Figure 2 : Jauges de déformation du modèle du blisk, côté extrados (version NEWAC).

Désormais, un nouvel extracteur de jauge de déformation plus conforme aux mesures expérimentales du banc d'essai de SNECMA est implanté dans notre modèle du blisk. L'implémentation de ce nouvel extracteur repose sur l'évaluation de la déformation entre deux points géométriques définis par l'utilisateur (voir Figure 3).

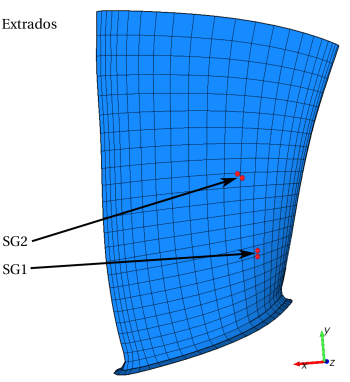Figure 3 : Jauges de déformation du modèle du blisk, côté extrados (nouveaux extracteurs).

Sur le plan de l'implémentation dans METAFOR, une nouvelle classe, nommée StrainGaugeValueExtractor et dérivant de la classe déjà existante GeoPointValueExtractor, a été créée. Cette nouvelle classe consiste, au travers de sa méthode computeLambda(), au calcul de l'Equation (1) à partir des positions des deux points géométriques définissant l'extracteur de jauge.

Les classes NatStrainGaugeValueExtractor, GLStrainGaugeValueExtractor et BiotStrainGaugeValueExtractor se chargent de remplir l'extracteur grâce la méthode extract() avec le calcul de la déformation 1D naturelle, de Green-Lagrange ou bien de Biot respectivement.

En détail, dans le seul cas de l'initialisation, nous procédons successivement de la manière suivante :

1. Nous recherchons l'élément fini le plus proche pour chacun des deux points géométriques.
2. Nous calculons les coordonnées réduites associées à chacun des deux points géométriques.
3. Nous calculons la distance $l_0$ entre les deux points géométriques à la configuration initiale.

Une fois l'initialisation terminée, à la fin de chaque pas de temps,

1. nous calculons les positions courantes des deux points géométriques Lagrangiens (calculées à partir des positions nodales courantes de l'élément fini le plus proche et des fonctions de forme évaluées en les coordonnées réduites),
2. nous calculons la distance $l$ entre les deux points géométriques de la jauge,
3. nous calculons le rapport $\lambda$ entre la distance courante et la distance initiale (cf. Equation (1)),
4. nous calculons la déformation 1D. L'utilisateur a le choix entre une déformation de Green-Lagrange (cf. Equation (2)), une déformation naturelle (cf. Equation (3)) et une déformation de Biot (cf. Equation (4)).

Il est à noter que la classe parente GeoPointValueExtractor a été adaptée afin de supprimer des perturbations des signaux de jauge induites par chaque redémarrage de l'intégration temporelle.

Equation (1) : \begin{equation} \lambda = \frac{l}{l_0} \label{eq:lambda} \end{equation}

Equation (2) : \begin{equation} \epsilon_{\text{GL}} = 0.5(\lambda^2 - 1) \label{eq:GLStrain} \end{equation}

Equation (3) : \begin{equation} \epsilon_{\text{Nat}} = \log (\lambda ) \label{eq:GLNat} \end{equation}

Equation (4) : \begin{equation} \epsilon_{\text{Biot}} = \lambda - 1 \label{eq:GLBiot} \end{equation}

En définitive, avec ce nouvel extracteur, l'évaluation de nos signaux de jauges est plus conforme aux mesures expérimentales du banc d'essai de SNECMA. Par ailleurs, nous sommes plus confiants en nos prédictions puisque nous nous affranchissons de toutes matrices de rotation (sources d'erreurs potentielles pour l'utilisateur). Enfin, il est à noter que cet extracteur est plus facile à définir pour l'utilisateur (seule la position géométrique initiale de deux points est à fournir et non plus quatre numéros de noeuds d'une maille).

Deux cas-tests sont ajoutés dans notre batterie pour tester les deux nouvelles fonctionnalités (impulsion sur une lame, extracteur de jauge de déformation et FFT du signal temporel de la jauge de déformation).

Ces deux cas-tests sont lancés par la méthode execFile car le répertoire mtFrequencyAnalysis.tests et tous ses sous-répertoires se lancent avec cette méthode.

Added : oo_meta\mtFEM\extractors\BiotStrainGaugeValueExtractor.h/.cpp
Added : oo_meta\mtFEM\extractors\StrainGaugeValueExtractor.h/.cpp
Added : oo_meta\mtFEM\extractors\GLStrainGaugeValueExtractor.h/.cpp
Added : oo_meta\mtFEM\extractors\NatStrainGaugeValueExtractor.h/.cpp
Added : oo_meta\mtFEMBase\ImpulseUniformLoading.h/.cpp
Added : oo_meta\mtFrequencyAnalysis\tests\ping\matlab\postPingTest.m
Added : oo_meta\mtFrequencyAnalysis\tests\ping\matlab\postPingTestFunctions.m
Added : oo_meta\mtFrequencyAnalysis\tests\ping\matlab\signalFrequencyAnalysis.m

Added : oo_meta\mtFrequencyAnalysis\tests\ping\beam3DFreeEas.py
Added : oo_meta\mtFrequencyAnalysis\tests\ping\beam3DFreeSri.py

— Yanick Crutzen 2016/07/12