• Prise en compte de la non-symétrie de la matrice de rigidité du modèle FEM dans la construction des matrices réduites des super-éléments de Guyan et de Craig-Bampton.
• Petites modifications dans la création des fichiers de sauvegarde des super-éléments

Dans Metafor, la matrice de rigidité du système n'est pas symétrique par défaut. En effet, certains termes ajoutés à la matrice la rendent non-symétrique, comme par exemple si on utilise des d'éléments EAS, lors d'un contact, lorsque les forces de Coriolis sont prises en compte, etc.

Etant donné que la théorie sur les super-éléments suppose toujours que la matrice de rigidité du système que l'on veut condenser est symétrique, certaines simplifications sont faites.

Le système d'équations associé au modèle EF que l'on souhaite condenser est le suivant : \begin{equation} \label{EQ:eq_mvt} \mathbf{M} \ddot{\mathbf{U}} + \mathbf{K} \mathbf{U} = \mathbf{F} \end{equation}

Afin de construire un modèle réduit, l'ensemble des DDLs du modèle FEM sont décomposés en des DDLs Retenus et des DDLs Condensés. Le système d'équation précédent s'écrit donc : \begin{equation} \label{EQ:eq_mvt_repartition} \left(\begin{array}{cc} \mathbf{M}_{RR} & \mathbf{M}_{RC} \\ \mathbf{M}_{CR} & \mathbf{M}_{CC} \end{array}\right) \left(\begin{array}{c} \ddot{\mathbf{U}}_R \\ \ddot{\mathbf{U}}_C \end{array}\right) + \left(\begin{array}{cc} \mathbf{K}_{RR} & \mathbf{K}_{RC} \\ \mathbf{K}_{CR} & \mathbf{K}_{CC} \end{array}\right) \left(\begin{array}{c} \mathbf{U}_R \\ \mathbf{U}_C \end{array}\right) = \left(\begin{array}{c} \mathbf{F}_R \\ \mathbf{0}_C \end{array}\right) \end{equation}

Un changement de base est ensuite réalisé afin de réduire la taille du système initial. Deux méthodes de réduction de modèle peuvent être formulées en fonction du changement de base effectué : la méthode de Guyan et celle de Craig-Bampton.

La formule du changement de base dans le cas de la méthode de Guyan est la suivante : \begin{equation} \label{EQ:eq_chgt_base_Guyan} \mathbf{U} = \left(\begin{array}{c} \mathbf{U}_R \\ \mathbf{U}_C \end{array}\right) = \left(\begin{array}{cc} \mathbf{I} \\ \Psi \end{array}\right) \mathbf{U}_R = \boldsymbol{\alpha} \ \mathbf{U}_R \end{equation} avec $\Psi = -\mathbf{K}_{CC}^{-1} \ \mathbf{K}_{CR}$, la matrice dont chaque colonne correspond à un mode statique de liaison.

En introduisant ce changement de base dans le système original, on obtient le système réduit de Guyan : \begin{equation} \label{EQ:eq_mvt_reduit_Guyan} \widetilde{\mathbf{M}} \ddot{\mathbf{U}}_R + \widetilde{\mathbf{K}} \mathbf{U}_R = \mathbf{F}_R \end{equation} avec : \begin{equation} \label{EQ:M_reduite_Guyan} \widetilde{\mathbf{M}} = \boldsymbol{\alpha}^t \ \mathbf{M} \ \boldsymbol{\alpha} = \mathbf{M}_{RR} + \Psi^t \ \mathbf{M}_{CR} + \mathbf{M}_{RC} \ \Psi + \Psi^t \ \mathbf{M}_{CC} \ \Psi \end{equation} \begin{equation} \label{EQ:K_reduite_Guyan} \widetilde{\mathbf{K}} = \boldsymbol{\alpha}^t \ \mathbf{K} \ \boldsymbol{\alpha} = \mathbf{K}_{RR} + \mathbf{K}_{RC} \ \Psi \end{equation}

La formule de changement de base dans le cas de la méthode de Craig-Bampton est la suivante : \begin{equation} \label{EQ:eq_chgt_base_CB} \mathbf{U} = \left(\begin{array}{c} \mathbf{U}_R \\ \mathbf{U}_C \end{array}\right) = \left(\begin{array}{cc} \mathbf{I} & \mathbf{0} \\ \Psi & \Phi \end{array}\right) \left(\begin{array}{c} \mathbf{Q}_R \\ \mathbf{Q}_N \end{array}\right) = \boldsymbol{\alpha} \ \mathbf{Q} \end{equation} avec $\Psi$ la matrice des modes statiques de liaison définie plus haut, et $\Phi$ la matrice dont chaque colonne correspond à un mode propre à interfaces fixes.

En introduisant ce changement de base dans le système original, on obtient le système réduit de Craig-Bampton : \begin{equation} \label{EQ:eq_mvt_reduit} \widetilde{\mathbf{M}} \ddot{\mathbf{Q}} + \widetilde{\mathbf{K}} \mathbf{Q} = \widetilde{\mathbf{F}} \end{equation} avec : \begin{equation} \label{EQ:M_reduite_CB_a} \widetilde{\mathbf{M}} = \boldsymbol{\alpha}^t \ \mathbf{M} \ \boldsymbol{\alpha} = \left(\begin{array}{cc} \widetilde{\mathbf{M}}_{RR} & \widetilde{\mathbf{M}}_{RN} \\ \widetilde{\mathbf{M}}_{NR} & \widetilde{\mathbf{M}}_{NN} \end{array}\right) \ \text{avec} \ \left\{\begin{array}{l} \widetilde{\mathbf{M}}_{RR} = \mathbf{M}_{RR} + \Psi^t \ \mathbf{M}_{CR} + \mathbf{M}_{RC} \ \Psi + \Psi^t \ \mathbf{M}_{CC} \ \Psi \\ \widetilde{\mathbf{M}}_{RN} = \widetilde{\mathbf{M}}^t_{NR} = \mathbf{M}_{RC} \ \Phi + \Psi^t \ \mathbf{M}_{CC} \ \Phi\\ \widetilde{\mathbf{M}}_{NN} = \Phi^t \ \mathbf{M}_{CC} \ \Phi \end{array}\right. \end{equation}

\begin{equation} \label{EQ:K_reduite_CB_a} \widetilde{\mathbf{K}} = \boldsymbol{\alpha}^t \ \mathbf{K} \ \boldsymbol{\alpha} = \left(\begin{array}{cc} \widetilde{\mathbf{K}}_{RR} & \widetilde{\mathbf{K}}_{RN} \\ \mathbf{0} & \widetilde{\mathbf{K}}_{NN} \end{array}\right) \ \text{avec} \ \left\{\begin{array}{l} \widetilde{\mathbf{K}}_{RR} = \mathbf{K}_{RR} + \mathbf{K}_{RC} \ \Psi\\ \widetilde{\mathbf{K}}_{RN} = \mathbf{K}_{RC} \ \Phi + \Psi^t \ \mathbf{K}_{CC} \ \Phi \rightarrow \text{Terme non nul !!}\\ \widetilde{\mathbf{K}}_{NN} = \Phi^t \ \mathbf{K}_{CC} \ \Phi \end{array}\right. \end{equation}

• Définition des blocs matrices utiles uniquement (certaines étaient définies et pas utilisées, et la matrice $\mathbf{K}_{RC}$ dont on a besoin n'était pas définie) :
  • Seul le bloc $NL/NL$ est utilisé lors d'une analyse fréquentielle classique ;
  • Seuls les blocs $BL/BL$, $BL/BF$, $BF/BL$, $BF/BF$ sont utilisés pour la construction d'un super-élément.

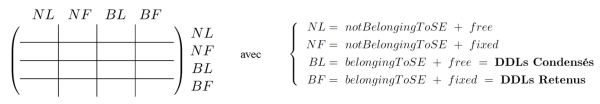
• Réécriture du destructeur de la classe en conséquence

• Suppression de certaines fonctions inutiles, comme par exemple updateBelongingFreeBelongingFreeTangStiffMatrix().

• Suppression de fonctions telles que fillConstrainedConstrainedMatrices() ou getConstrainedConstrainedMassMatrix(), par exemple, qui ne sont appelées que lors de la création d'un super-élément et qui sont donc directement remplacées par les fonctions spécifiques correspondantes fillBelongingConstrainedBelongingConstrainedMatrices() et getBelongingConstrainedBelongingConstrainedMassMatrix().

• Modification des noms de fonctions suite aux modifications faites dans MechanicalMatrices.

• Ajout du calcul des blocs $\mathbf{M}_{RC}$ et $\mathbf{K}_{RC}$ via la fonction fillBelongingConstrainedBelongingFreeMatrices().

• Modification du calcul du vecteur kRCPsiI : kRCPsiI = kRC*(*psiI) au lieu de kRCPsiI = kCR.computeTransposeProduct(*psiI) qui supposait que kRC = kCR^t, i.e. que k était symétrique.

• Modification des noms de fonctions suite aux modifications faites dans MechanicalMatrices.

• Ajout du calcul des blocs $\mathbf{M}_{RC}$ et $\mathbf{K}_{RC}$ via la fonction fillBelongingConstrainedBelongingFreeMatrices().

• Modification du calcul du vecteur kRCPsiI : kRCPsiI = kRC*(*psiI) au lieu de kRCPsiI = kCR.computeTransposeProduct(*psiI) qui supposait que kRC = kCR^t, i.e. que k était symétrique.

• Ajout du calcul du bloc $\widetilde{\mathbf{K}}_{RN}$ dans la fonction execute(), via le calcul du vecteur kRCPhiI notamment.

• Modification de la fonction structToElem() qui remplit la variable superElemStiffMatrix suite à l'ajout du bloc $\widetilde{\mathbf{K}}_{RN}$.

• Modification de la fonction python createPyFileForSuperElemUse dans les fichiers suivants :

\oo_meta\mtSuperElement\tests\tools\utilities.py
\oo_nda\abrawal\banc18ER\tools\utilities.py

L'index est maintenant défini comme un argument dans le constructeur de la classe SuperElementBaconImporter, ce qui est moins dangereux. Par conséquent, le constructeur a été modifié et la fonction setIndex() a été supprimmée.

• Modification de l'écriture des fichiers de sauvegarde concernant le type de super-élément 2D ou 3D. Le type étant connu au moment où on crée le fichier de sauvegarde, la fonction saveRetainedNodes() du fichier SuperElement.cpp a été modifiée.

• Par conséquent, modification des cas-tests de mtSuperElement.

Renamed: mtSuperElement\tests\tools\Beam.py -> beamBuilder.py
Renamed: mtSuperElement\tests\tools\toolsVE.py -> valueExtractors.py

Deleted: mtSuperElement\tests\tools\superElement.py
Deleted: mtSuperElement\tests\tools\superElementNew.py
Deleted: abrawal\banc18ER\tools\superElements18ER.py

Des nouveaux cas-tests suivront…

— Claire Hennuyer 2016/06/23