Table of Contents
Commit 2016-02-04
DampedAlphaGeneralizedTimeIntegration : le retour…
Amélioration du schéma ''DampedAlphaGeneralizedTimeIntegration''
- Calcul des matrices d'amortissement sur les éléments de masse et de ressort
- Déplacement du taux de $K$ (
DAMPSTIFF) ou $M$ (DAMPMASS) dans la matrice d'amortissement du schéma vers les propriétés élémentaires. - Possibilité de faire varier ces taux en fonction du temps (via prp.depend)
- Choix du moment de la mise à jour de la matrice d'amortissement via la fonction de schéma
ti.setDampingMatrixUpdate(DMUxxxxx)avecDMUINIT: matrice calculée sur la configuration initiale (auquel cas, la dépendance via les propriétés n'auront pas d'effet!!!)DMUPERSTAGE: matrice recalculée à chaque changement de stage (permet d'avoir une phase d'équilibrage post mise à forme)DMUPERSTEP: matrice recalculée à chaque pas de temps (calcul basé sur la configuration équilibrée précédente) : indispensable dans le cas de simulation tournante (voir illustration ci dessous)
- Notons :
- Que la matrice de raideur utilisée est celle de l'élément dans son état au moment du calcul (tenant compte de la plasticité, la viscosité élastique ou plastique, l'endommagement,…). L'implémentation d'une raideur élastique serait, il me semble mieux adaptée…
- L'amortissement est basé sur une représentation linéaire ($C*v$), et s'articule assez mal dans un cadre non linéaire (le développement d'une fonction d'amortissement $FDamp$ et de sa raideur associée permettrait une meilleure interaction)
- Le cout de la mise à jour de la matrice d'amortissement à chaque pas est non négligeable (calcul de la matrice de raideur de chaque élément, la matrice de masse étant invariable) et pas (encore) parallélisé
- Dans un premier temps, j'avais interfacé la mise à jour de la matrice d'amortissement dans un cadre remaillage/ale mais ca devrait découler du
DMUPERSTEP
- Calcul de l'énergie dissipée par les ressorts (quand ils ont un amortisseur), et du matériau Visco-élastique :
KelvinVoigtViscoElastHypoMaterial. - todo :
GeneralizedMaxwellViscoElastHypoMaterial(Cristian ?)NortonHoffPHypoMaterialet dérivés (Yves)
- Renaming fonction :
- computePlasticDissipation → computeDissipatedEnergy
Illustration 1 : Système masse ressort excité à sa base
Soit :
- un ressort de longueur 1
- de raideur K = 1.0e4
- une masse concentrée à son extrémité (pt2) M = 1.0e-4
soumis à
- une excitation harmonique à la base (pt1) (freq = 1591)
- d'amplitude = 1.0e-2
- sur 10 cycles
observation sur
- les 10 cycles d'excitation
- 10 cycles supplémentaires
Quel que soit la méthode, le paramètre d'amortissement est toujours choisi pour obtenir un amortissement de 10% !!!
On observe :
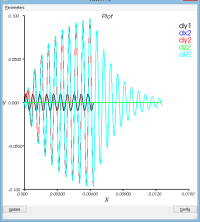
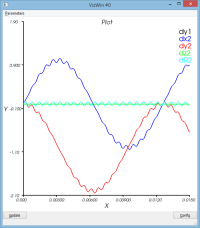
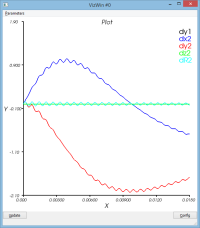
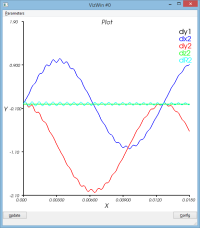
- Le déplacement des 2 points caractéristiques
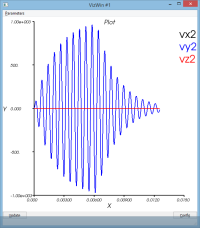
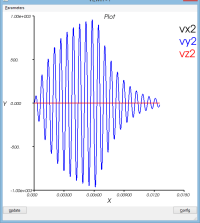
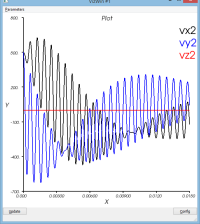
- La vitesse au point 2
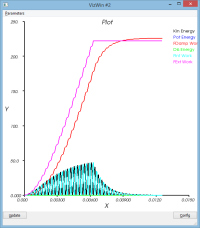
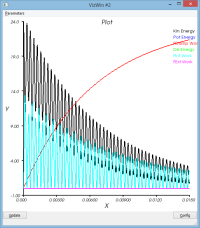
- Le bilan énergétique
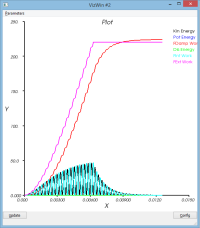
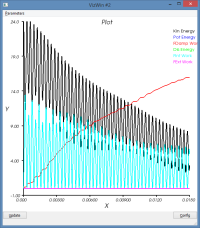
système non amorti : massSpring3d.py
On observera l'amplification de la réponse (on est à la fréquence propre du système) durant la phase d'excitation et la perte d'énergie liée au schéma d'intégration sur la phase de maintient (bilan énergétique)
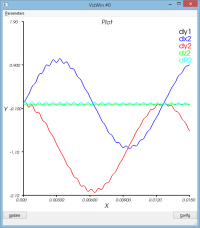
amortissement en raideur : massSpring3dDampK.py
- dampK = 1.0e-5
On observe une très forte modération de l'amplification de la réponse (même si amplification il y a encore). De la même part, on observe aussi que l'énergie dissipée par l'amortissement (WorkFDamp) dépasse l'énergie amenée à ce même système (WorkFExt). Je n'ai pas compris d'où vient cette différence (observable aussi sur des éléments volumiques).
amortissement en masse: massSpring3dDampM.py
- dampM = 1.0e3
Le taux d'amortissement ayant été réglé identiquement, et la réponse étant unique, il n'y a pas de différence entre les méthodes d'amortissement.
dashpot : massSpring3dDashPot.py
- CSpring = 1.0e-1
La dissipation du dash-pot ayant été réglé de manière à dissiper 10% de l'énergie, il n'y a pas de différence entre l'usage du dash-pot et du schéma amorti.
Illustration 2 : Système masse ressort en rotation
Soit le même système mais
- dont la base est fixe
- dont l'extrémité libre est soumise à une vitesse initale générant à la fois rotation et oscillation :
- V0X = 5.0e2
- V0Y = 5.0e2
- Observation sur le temps d'un peu plus d'1 tour (1.5e-2)
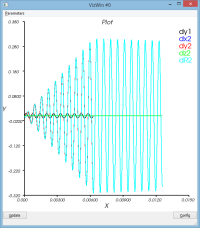
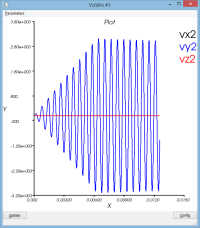
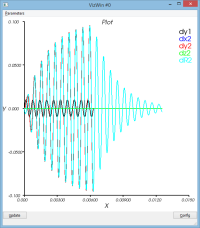
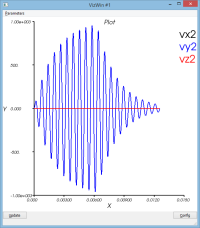
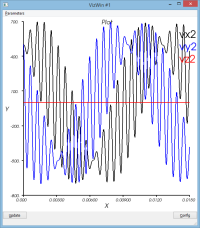
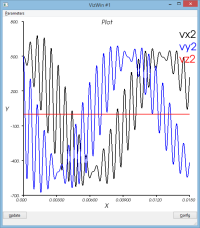
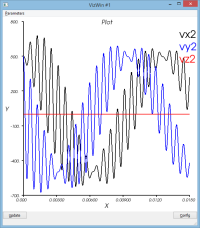
système non amorti : massSpring3dV0XY.py
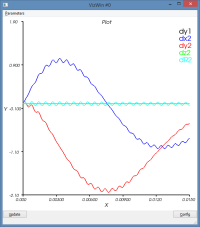
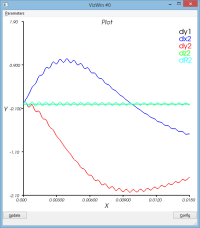
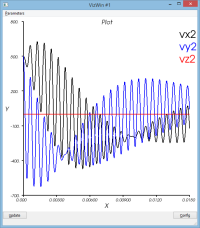
Le mouvement de la masse se décompose entre
- un mouvement de rotation de l'ensemble du dispositif autour du pt1
- un mouvement d'oscillation de la masse (pt2) par rapport au pt2 (voir courbe dR)
Le schéma dissipe un peu de l'énergie qui lui a initialement été confiée (peu significatif)
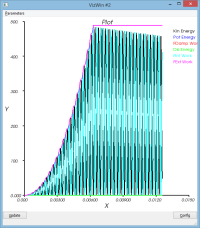
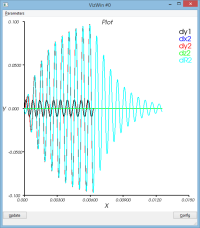
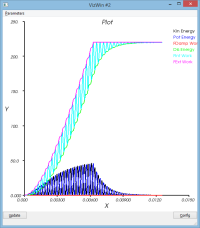
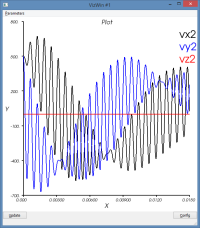
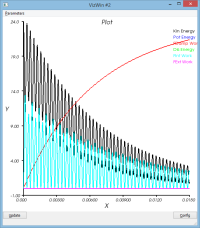
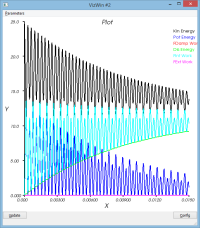
amortissement en raideur : massSpring3dV0XYDampK.py
- dampK = 1.0e-5
Si on ajoute de l'amortissement sur le terme de raideur, on observe
- que le mouvement d'ensemble est globalement conservé
- mais que le mouvement vibratoire est lui plus amorti (voir courbe dR et l'enveloppe suppérieure de la courbe d'énergie cinétique alors que l'enveloppe inférieure reste constante)
C'est le comportement attendu (il est comparable à l'ajout d'un dash-pot sur le ressort)
amortissement en raideur : massSpring3dV0XYDampKNoUpdt.py
- dampK = 1.0e-5
- matrice d'amortissement calculée sur la configuration initiale uniquement
Si on oublie de mettre à jour la matrice d'amortissement à chaque pas de temps, les grandes rotations du ressort (mouvement d'ensemble) désaligne raideur et amortissement. Le mouvement d'ensemble est dès lors ralenti. L'énergie dissipée montre des oscillations lorsque le ressort est aligné verticalement.
DANS CE CAS, ON NE CALCULE PAS DU TOUT CE QUE L'ON CROYAIT CALCULER !!!
Le calcul de la matrice d'amortissement à chaque pas de temps a un cout (négligeable dans ce cas, mais sur un gros système, ca pourrait finir par couter!!!)
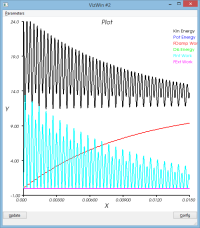
amortissement en masse: massSpring3dV0XYDampM.py
- dampM = 1.0e3
L'amortissement en masse dissipe de l'énergie tant sur le mouvement d'ensemble que sur le mouvement de vibration (les enveloppes supérieures et inférieures de l'énergie cinétique montrent toutes deux une forte décroissance et se rapprochent) contrairement à l'amortissement en raideur.
amortissement en raideur : massSpring3dV0XYDampMNoUpdt.py
- dampM = 1.0e3
- matrice d'amortissement calculée sur la configuration initiale uniquement
Les composantes de la matrice de masse ne dépendant pas de la direction (X,Y ou Z), elle est donc indirectionnelle et le calcul de la matrice d'amortissement ne dépendra donc pas de la position de la masse.
dashpot : massSpring3dV0XYDashPot.py
- CSpring = 1.0e-1
L'amortissement via un dash-pot montre un comportement similaire à l'amortissement en raideur (avec remise à jour de la matrice d'amortissement à chaque pas de temps). Etant donné le calcul de la dissipation sur la configuration actuelle, le dash-pot doit d'ailleurs être plus précis que l'amortissement en raideur (dont la raideur est celle de la configuration initale).
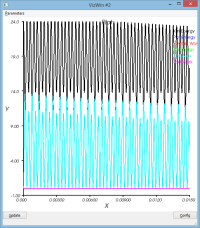
Illustration 3 : poutre encasté-libre
système illustré au commit 2525 avec 2*2*1 éléments EAS.
Objectif : voir l'influence de la mise à jour de la matrice d'amortissement sur le temps de calcul (le système ne subissant ni grandes déformation, ni de grande rotation, peu d'influence sur le résultat).
temps de calcul
| STP | ITE | CPU | |
| cantNl2EasNoDamp | 2000 | 2004 | 4.02 |
| cantNl2EasM0Km6 | 2000 | 2002 | 4.22 |
| cantNl2EasM0Km6Updt | 2000 | 2002 | 5.84 |
| cantNl2EasM4K0 | 2000 | 2004 | 4.03 |
| cantNl2EasM4K0Updt | 2000 | 2004 | 4.03 |
| cantNl2EasM4Km6 | 2000 | 2002 | 4.18 |
| cantNl2EasM4Km6Updt | 2000 | 2002 | 5.72 |
Sur le présent test (beaucoup trop faiblement maillé), le remplissage de la matrice d'amortissement à partir de la matrice de masse n'est pas significatif en terme de temps de calcul, alors que le calcul de la matrice de raideur élémentaire pour mettre à jour la matride d'amortissement est déjà clairement mesurable sur un test limité (⇒ pourrait devenir très important sur de gros tests!!!).
CONCLUSION
- Il est TRES important de bien penser l'amortissement (et sa mise à jour) selon l'obectif de la simulation
- La définition des ratios d'amortissement (en masse ou en raideur) influe aussi sur la réponse fréquentielle comme illustré au commit 2525 (amortissement des HF ou des BF).
- Une mise à jour trop fréquente de l'amortissement peut finir par couter
- la raideur utilisée étant totale ⇒ en EP, la raideur apparente baisse fortement, cela pourrait avoir un effet perturbant sur le système (ou peut être intéressant selon ce qu'on simule !!!)
Divers
- Abrawal/Banc18ER :
- Normalisation du paramètre de visco-élasticité par rapport à $2G$ (alors que auparavant on normalisait par rapport à $E$)
- Ajout des options pour utiliser le schéma $\alpha$Généralisé avec amortissement dans le jeux de donnée du banc, latex, …
SetStage:- ajout de 2 booléen dans la classe
StageManagerde manière à ce que la fonctionSetStagene renvoie plus rien, mais mette à jour ses variables internes que l'on peut interroger de l'extérieur pour savoir si l'on a changé de stage (et donc le cas échéant recalculer la matrice d'amortissement) ou si on doit remettre à jour les connections …
Fichiers ajoutés/supprimés
Added : Deleted :
Tests ajoutés/supprimés
Added : oo_meta\apps\dampedAlphaGenTI\cantNl2EasM4Km6Updt.py Added : oo_meta\apps\dampedAlphaGenTI\cantNl2EasM4K0Updt.py Added : oo_meta\apps\dampedAlphaGenTI\cantNl2EasM0Km6Updt.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3d.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dDashPot.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dDampK.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dDampM.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dV0XY.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dV0XYDashPot.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dV0XYDampK.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dV0XYDampKNoUpdt.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dV0XYDampM.py Added : oo_meta\apps\dampedAlphaGenTI\massSpring3dV0XYDampMNoUpdt.py Added : oo_nda\abrawal\banc18ER\battery\casingRotDamped.py Renamed : Deleted :
— Luc Papeleux 2016/02/03