Table of Contents
Commit 2014-03-19
Modifications
Ajout des matériaux de contact thermomécanique collant et avec frottement selon Tresca
J'ai ajouté le matériau thermomécanique collant et avec frottement selon Tresca. Par la même occasion, j'ai documenté un peu plus tous les matériaux thermomécaniques de contact :
TmFrictionlessContactMaterial
Description
Loi de contact thermomécanique sans frottement.
Le flux de chaleur $q_{N}$ normal à l'interface de contact (sortant de la surface esclave) est déterminée par
$$q_{N} = h_c \left(p_{N} \right) \left(T^{S} - T^{M}\left(\bf{\xi}^{S}\right)\right), $$
où
- $p_{N}$ est la pression de contact,
- $T^{S}$ est la température du nœud esclave,
- $T^{M}\left(\bf{\xi}^{S}\right)$ est la température du point sur la surface maître qui correspond à la projection la plus proche du nœud esclave sur la surface maître,
- $h_c$ est le coefficient de résistance thermique de conduction.
Le coefficient de résistance thermique de conduction $h_c$ est modélisée par
$$h_c \left(p_{N} \right) = h_{c0} \left(\frac{p_{N}}{H_v}\right)^{w}, $$
où
- $H_v$ la dureté du matériau selon Vickers,
- $w$ est un exposant,
- $h_{c0}$ le coefficient de résistance thermique de conduction nominale.
Paramètres
| Nom | Code Metafor | Type de dépendance |
|---|---|---|
| Pénalité normale | PEN_NORMALE | TM |
| Profondeur de détection du contact | PROF_CONT | - |
| Coefficient d'échange nominal | CTM_H_NOMINAL | - |
| Exposant de la loi d'échange | CTM_EXPONENT_E | - |
| Dureté du matériau | CTM_HARDNESS | - |
| Type de contact | TYPE_CONT | - |


TmStickingContactMaterial
Description
Loi de contact thermomécanique collant.
Paramètres
| Nom | Code Metafor | Type de dépendance |
|---|---|---|
| Pénalité normale | PEN_NORMALE | TM |
| Pénalité tangente | PEN_TANGENT | TM |
| Profondeur de détection du contact | PROF_CONT | - |
| Coefficient d'échange nominal | CTM_H_NOMINAL | - |
| Exposant de la loi d'échange | CTM_EXPONENT_E | - |
| Dureté du matériau | CTM_HARDNESS | - |
| Type de contact | TYPE_CONT | - |


TmCoulombContactMaterial
Description
Loi de contact thermomécanique avec frottement de Coulomb.
Paramètres
| Nom | Code Metafor | Type de dépendance |
|---|---|---|
| Pénalité normale | PEN_NORMALE | TM |
| Pénalité tangente | PEN_TANGENT | TM |
| Profondeur de détection du contact | PROF_CONT | - |
| Coefficient de frottement statique | COEF_FROT_STA | TM |
| Coefficient de frottement dynamique | COEF_FROT_DYN | TM |
| Coefficient d'échange nominal | CTM_H_NOMINAL | - |
| Exposant de la loi d'échange | CTM_EXPONENT_E | - |
| Dureté du matériau | CTM_HARDNESS | - |
| Type de contact | TYPE_CONT | - |


TmTrescaContactMaterial
Description
Loi de contact thermomécanique avec frottement de Tresca.
Paramètres
| Nom | Code Metafor | Type de dépendance |
|---|---|---|
| Pénalité normale | PEN_NORMALE | TM |
| Pénalité tangente | PEN_TANGENT | TM |
| Profondeur de détection du contact | PROF_CONT | - |
| Coefficient de frottement statique | COEF_FROT_STA | TM |
| Coefficient de frottement dynamique | COEF_FROT_DYN | TM |
| Coefficient d'échange nominal | CTM_H_NOMINAL | - |
| Exposant de la loi d'échange | CTM_EXPONENT_E | - |
| Dureté du matériau | CTM_HARDNESS | - |
| Type de contact | TYPE_CONT | - |
Le seuil est généralement calculé par $m\,\sigma_0\,/\sqrt{3}$ où m est le coefficient de frottement de Tresca et $\sigma_0$ est la limite élastique en traction du matériau.


Bug - Éléments de contact thermomécanique
L'aire de contact d'échange thermique n'est pas la même que l'aire de contact associée à chaque nœud esclave dans le cas de la méthode area in contact (cf. Thèse de Laurent Adam). Donc j'ai dû adapter le calcul de la pression de contact intervenant dans le coefficient de résistance thermique de conduction (voir début du commit). De fait, on peut utiliser les éléments de contact thermomécanique sans area in contact, dès lors on divise la force de contact par l'aire de contact d'échange thermique pour obtenir une pression de contact “équivalente”.
Divers - Gestion des itérations mécaniques/thermiques
J'ai ajouté la possibilité de désactiver le critère d'arrêt des itérations mécaniques et/ou thermiques
mim/tim.setPreviousResidualsDecreaseCriterion(False)
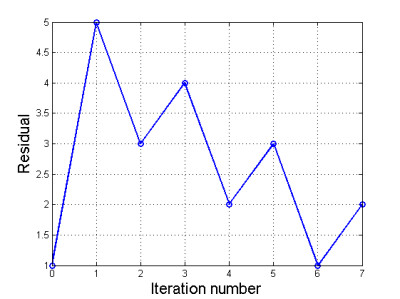
,lorsque le résidu ne diminue pas suffisamment sur les six dernières itérations :
$$ Residual(i-2) \leq 0.9 Residual(i), \; \text{pour} \; i = 3:6. $$
Le vecteur $Residual$ contient les $6$ derniers résidus.
Le critère d'arrêt est activé uniquement si on a effectué 6 itérations mécaniques et/ou thermiques (La phase de prédiction du schéma d'intégration est prise en considération, puisque l'on calcule le résidu).
La convergence du résidu est dès lors non monotone, étant donné que l'on ne compare pas deux résidus successifs. Autrement dit, le résidu peut augmenter à condition qu'il diminue suffisamment par la suite, sinon on a une divergence.
Il est intéressant de désactiver ce critère d'arrêt, lorsque l'on désire comparer des méthodes de calcul sur des cas tests académiques.
Cas Test
J'ai ajouté 4 nouveaux cas-tests pour tester le contact thermomécanique pour les 4 matériaux de contact disponibles actuellement. Le cas test est l'écrasement d'un bloc en état plan déformation avec un plan rigide. Pour le matériau sans frottement et collant, il y a une différence de température entre le plan rigide et le bloc, tandis que pour les cas avec frottement de Coulomb et de Tresca, il n'y en a pas et donc les évolutions de température sont principalement dues à la dissipation par frottement.
Fichiers ajoutés/supprimés
[r]: [a]:mtMaterials/boundaries/TmStickingContactMaterial.h [a]:mtMaterials/boundaries/TmStickingContactMaterial.cpp [a]:mtMaterials/boundaries/TmTrescaContactMaterial.h [a]:mtMaterials/boundaries/TmTrescaContactMaterial.cpp
Tests ajoutés/supprimés
[r]: [a]:apps/contactTm/RdEplBlockFrictionLess.py [a]:apps/contactTm/RdEplBlockSticking.py [a]:apps/contactTm/RdEplBlockCoulomb.py [a]:apps/contactTm/RdEplBlockTresca.py
— Gaëtan WAUTELET 2014/03/18