Commit 2013-06-14

La méthode Area In Contact associe une aire à chaque noeud esclave (élément de contact). Ainsi, on peut tenir compte de la densité du maillage sur la frontière de contact (petite maille à côté de grosse maille). Dès lors, la force de contact agissant sur le noeud esclave, dans le cas d'un contact sans frottement (pour faire simple), est donnée par

$\vec{F}^{(s)} = - t_n A_s \vec{n}^{(m)}$

où

- (s) indique l'esclave.
- (m) indique le maître.
- $A_s$ est l'aire de contact nodale.
- $\vec{n}$ est la normale extérieure unitaire.
- $t_n$ est la pression de contact.

Dans le cadre de la méthode de la pénalité classique, la pression de contact est donnée par

$t_n = C_n g_n $

où

- $C_n$ est le coefficient de pénalité.
- $g_n$ est la distance signée du noeud esclave par rapport à la surface maître.

J'ai raccourci le nom des paramètres disponibles pour la méthode AREAINCONTACTMETHOD :

• AIC_METHOD_GEOMETRIC devient AICM_GEOPHYS.
• AIC_METHOD_CONSISTENT devient AICM_CONS.

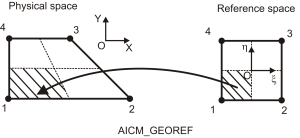
et j'ai ajouté une dernière méthode de calcul de l'aire de contact nodale dénommée AICM_GEOREF.

Dans le cas de quadrangles bilinéaires en 3D, l'aire de contact nodale d'un nœud esclave est égale à la somme des aires “pondérées” des quadrangles incidents à ce nœud. Pour chaque quadrangle bilinéaire, cette aire “pondérée” est une portion de l'aire du quadrangle dans l'espace physique correspondant à un quart de l'aire du quadrangle de référence dans l'espace de référence, comme il est illustré sous forme hachurée sur la figure suivante.

L'aire de contact nodale est un facteur de pondération, dont les dimensions sont celles d'une aire. On distingue les différents cas suivants :

• En état plan déformation, les trois méthodes donnent la même valeur de l'aire de contact nodale dans le cas d'éléments finis linéaires (Bord de triangle linéaire ou de quadrangle bilinéaire).

• En modélisation axisymétrique, la méthode AICM_GEOREF équivaut à celle AICM_GEOPHYS, et donne une aire de contact nodale différente de la méthode AICM_CONS dans le cas d'éléments finis linéaires (Bord de triangle linéaire ou de quadrangle bilinéaire).

• En 3D, les trois méthodes donnent la même valeur de l'aire de contact nodale dans le cas de triangle linéaire (Face de tétraèdre linéaire ou de pentaèdre “linéaire”).

• En 3D, les trois méthodes donnent en général des valeurs différentes de l'aire de contact nodale dans le cas de quadrangle bilinéaire (Face d'hexaèdre trilinéaire ou de pentaèdre “linéaire). Cependant, si tous les nœuds du quadrangle bilinéaire se trouvent dans un même plan et que celui-là prend la forme d'un carré ou d'un rectangle, les trois méthodes donne la même valeur de l'aire de contact nodale.

Lors de la définition d'une interaction de contact rigide déformable pilotée en force, les éléments de contact possèdent deux nœuds au niveau élémentaire :

• Nœud 1 : Nœud esclave associé à un nœud de l'entité géométrique esclave sur laquelle l'interaction de contact est définie,
• Nœud 2 : L'unique nœud maître associé à la matrice rigide de contact.

Par le principe de l'action et réaction, la force de contact élémentaire agissant sur le nœud 2 (nœud maître) est égale et opposée à la force de contact élémentaire agissant sur le nœud 1 (nœud esclave).

Dès lors, il est normal d'obtenir une force résultante extérieure nulle lors de l'utilisation de l'extracteur

  valueExtractor = InteractionValueExtractor (interaction, natureId, vectorId=GEN_EXT_FORC)

avec interaction = Référence vers l'interaction de contact rigide déformable pilotée en force; natureId = (TX, TY, TZ) et vectorId = GEN_EXT_FORC.

Désormais, il est possible de l'utiliser pour obtenir la composante de la force résultante de contact exprimée dans les axes structuraux, sans devoir passer par les forces extérieures agissant sur les nœuds de l'entité esclave.

Lors que l'on ouvre l'object browser, nous pouvons avoir accès à des informations sur les objets instanciés lors du chargement du cas-test.

On peut modifier le contenu des informations à l'aide le fonction suivante disponible dans la majorité des objets :

void write(std::ostream &out, const Indentor &indent=Indentor(), const WOpt::flags &opts=WOpt::all);

J'ai indiqué des informations sur des objets géométriques et sur les interactions (surtout celles de contact) :

- Interactions :

- Surface NURBS :

C'est vraiment très utile et ça permet de vérifier le valeur des paramètres réellement contenus dans les objets instanciés.

La génération du maillage sur une side avec une surface avec le mailleur transfini 2D procède de la manière suivante :

• Détermination de la position du nœud sur une surface bilinéaire de Coons construite à partir du wire de la side, pour les paramètres (u,v) donnés
• Projection de ce nœud sur la surface

Cependant, l'opérateur de projection modifie les valeurs (u,v) données en entrée par référence (Métrique de la surface réelle et la surface bilinéaire sont différentes en général). Si on boucle sur le paramètre u et puis sur le paramètre v, on constate que le paramètre u change pour chaque valeur de v suite à l'utilisation de l'opérateur de projection. L'ajout de gardiens adéquats a permis de corriger cette erreur.

Sans cette correction, on observait des zig-zags dans la position des nœuds projetés sur la surface de la side ou le maillage était totalement distordu.

J'ai constaté que les critères de convergence n'étaient pas suffisamment précis dans le cas de la génération d'un maillage sur une surface. En effet, une faible variation des paramètres u et v dans l'espace paramétrique peut correspondre à une variation non négligeable de la position du point S(u,v) de la surface dans l'espace physique.

Je me suis basé sur les recommandations aux pages 233 et 234 du bouquin de référence suivant The NURBS Book (second edition, 1997), Les Piegl and Wayne Tiller.

Il est désormais possible de sélectionner des nœuds sur une partie d'une sphère au moyen d'une sélection dans un secteur sphérique.

Si on désire récupérer tous les nœuds dans le secteur sphérique de centre (Cx,Cy,Cz), de rayon minimum rMin et maximum rMax, d'angle azimutale minimum thetaMin et maximum thetaMax, et d'angle d'élévation minimum phiMin et maximum phiMax :

 
group.addMeshPoints(SectorSphericalSelector(Cx, Cy, Cz, rMin, rMax, thetaMin, thetaMax, phiMin, phiMax)) 

Remarque : les angles sont calculés par rapport au système d'axes structuraux translatés au centre de la sphère. L'angle d'élévation varie de $-\frac{\pi}{2}$ à $\frac{\pi}{2}$ et l'angle azimutale varie de $0.0$ à $2 \pi$.

La méthodologie de construire une grille de $nbel$ intervalles sur une courbe commence par la spécification de la distribution des points sur cette dernière. Ceci revient à spécifier la distribution du paramètre de la courbe ${u(\xi) \; 0 \leq \xi \leq nbel+1}$ dans l'espace paramétrique, qui correspond aux points de la courbe ${\boldsymbol{x}(u) \; 0 \leq u \leq 1}$ dans l'espace physique. La tâche finale est de déterminer ${u(\xi) \; 0 \leq \xi \leq nbel+1}$ tel que ${\boldsymbol{x}(u(\xi)) \; 0 \leq \xi \leq nbel+1}$ est une bonne paramétrisation de la courbe $\boldsymbol{x}(u)$.

La recherche de la fonction $u(\xi)$ revient à trouver la fonction $\xi(u)$. Avec la définition $\rho(u) = \frac{d\xi}{du}$,

$$ \xi(u) = \int_0^u \rho(w) dw. $$

Dans le cas hybride, un ensemble plus complexe de considérations physiques est pris en compte dans la construction d'une fonction de densité des points de la grille, $\rho(u)$. Les approches possibles incluent les suivantes :

• Distribution uniforme de la longueur d'arc où les points de la grille sont séparés par des distances égales dans l'espace physique. Dans ce cas, la densité des points de la grille doit être proportionelle au taux de variation de la longueur d'arc, c'est à dire $\rho(u) \propto \left\| \frac{d\boldsymbol{x}}{du} \right\| $.
• Distribution uniforme de la longueur d'arc pondérée par la courbure, où les points de la grille sont concentrés dans les régions de forte courbure. Pour ce cas-là, la fonction de densité des points de la grille prend la forme suivante

$$\rho(u) \propto \kappa(u) \left\| \frac{d\boldsymbol{x}}{du} \right\| $$ où $\kappa(u)$ est la courbure de la courbe $\boldsymbol{x}$ en $u$.

• Attraction de la grille vers un point d'attraction $u^{*}$ dans l'espace paramétrique (correspondant au point $\boldsymbol{x}^{*} = \boldsymbol{x}(u^{*})$ dans l'espace physique). Un cas typique est $u^{*}=0$ ou $u^{*}=1$, quand on désire capter une échelle de petite taille à une des extrémités de la courbe. Alternativement, $0< u^* < 1$ concentrait le raffinement près d'un point à l'intérieur de la courbe. Pour ces cas-là, un bon choix pour $\rho(u)$ est :

$$ \rho_{u^{*}} (u) \propto \frac{1}{\sqrt{(k (u-u^{*}))^2 +1} } $$

où $k$ est un facteur d'attraction qui détermine l'intensité d'attraction vers $u^{*}$.

En pratique, il est plus que probable que l'utilisateur désire une fonction hybride de densité de points de la grille, qui est une combinaison linéaire de plusieurs fonctions de densité décrites ci-dessus. Dans ce cas, plusieurs fonctions de densité $\rho_i(u)$ peuvent être combinées, chacune normalisée de manière à ce que $\int_0^1 \rho_i(u) \, du = \xi(1)-\xi(0) = m$. Etant donné les constantes positives $\lambda_i$ telles que $\sum_i \lambda_i=1$, on construit $\rho(u) = \sum_i \lambda_i \rho_i(u)$ qui est une fonction de densité de points de la grille avec une normalisation adéquate. Cette fonction hybride de densité va migrer les points de la grille dans les régions où une des fonctions $\rho_i(u)$ nécessite un raffinement. En utilisant ce concept, il est possible de répartir les points de la grille sur base des critères hybrides de longueur d'arc, de courbure et d'attraction vers un ensemble ${u_i^*}$ de points distincts.

Finalement, si on donne les poids $\lambda_s$, $\lambda_{\kappa}$, les points $\{u_i^* \; | \; 0 \leq u_i^* \leq 1, \; 1 \leq i \leq p\}$, les poids $\{\lambda_i, \; 1 \leq i \leq p\}$ et les facteurs d'attraction $\{k_i, \; 1 \leq i \leq p\}$ où $\lambda_s+\lambda_{\kappa}+\sum_{i=1}^p \lambda_i =1$, on génère une distribution de $nbel+1$ points $u_0, u_1, \ldots, u_{nbel+1}$ qui sont simultanément concentrés au voisinage des points d'attraction $\{u_i^*\}$, positionnés dans les régions de forte courbure, et positionnés de manière à éviter de grands écarts sur la longueur d'arc.

Sous Metafor, le mailleur HybridDensityMesher1D est interfacée sous la forme suivante :

Mesher = HybridDensityMesher1D(curveset(numero),p)                              
Mesher.execute(nbel,lambdaS,lambdaK,cells)

Si on désire concentrer les mailles autour d'un point d'attraction, nous pouvons utiliser les commandes suivantes avant l'opération .execute():

Mesher.pushAttractorPt(uJ)
Mesher.pushWeight(lambdaJ)
Mesher.pushStrength(kJ)

Finalement, il existe une commande interfacée pour pouvoir débugger le mailleur :

Mesher.setVerbose()

Exemples

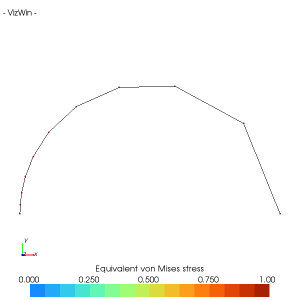
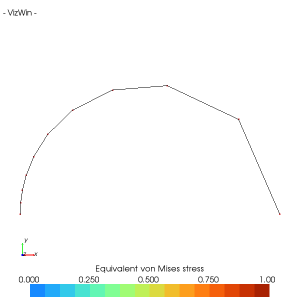
Soit le demi cercle de rayon unitaire décrit par une courbe NURBS. On décide de la discrétiser avec 10 mailles et de concentrer les mailles tout près de l'extrémité gauche :

SimpleMesher1D

Rapport de 10 entre la dernière et la première maille

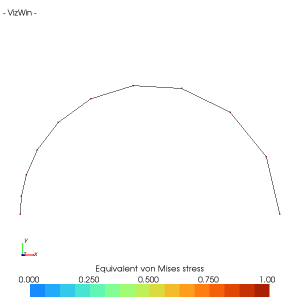
HybridDensityMesher1D

Paramètres du point d'attraction uJ = 0.0 : lambdaJ = 1.0 et kJ = 10.0

Paramètres du mailleur : lambdaS = 0.0, lambdaK = 0.0

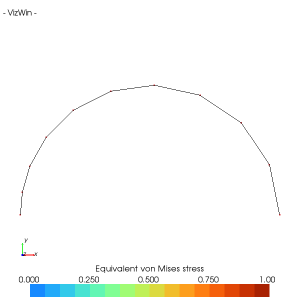
HybridDensityMesher1D

Paramètres du point d'attraction uJ = 0.0 : lambdaJ = 0.5 et kJ = 10.0

Paramètres du mailleur : lambdaS = 0.5, lambdaK = 0.0

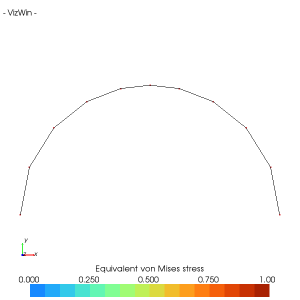
HybridDensityMesher1D

Paramètres du point d'attraction uJ = 0.0 : lambdaJ = 1.0/3.0 et kJ = 10.0

Paramètres du mailleur : lambdaS = 1.0/3.0, lambdaK = 1.0/3.0

Soit le demi cercle de rayon unitaire décrit par une courbe NURBS. On décide de la discrétiser avec 10 mailles et de concentrer les mailles tout près du point milieu :

HybridDensityMesher1D

Paramètres du point d'attraction uJ = 0.5 : lambdaJ = 1.0/3.0 et kJ = 10.0

Paramètres du mailleur : lambdaS = 1.0/3.0, lambdaK = 1.0/3.0

Soit la spline cubique suivante. On décide de la discrétiser avec 20 mailles et de concentrer les mailles tout près de l'extrémité gauche :

SimpleMesher1D

Rapport de 10 entre la dernière et la première maille

HybridDensityMesher1D

Paramètres du point d'attraction uJ = 0.0 : lambdaJ = 0.5 et kJ = 50.0

Paramètres du mailleur : lambdaS = 0.25, lambdaK = 0.25

Ce mailleur est indépendant du paramétrage de la courbe contrairement au SimpleMesher1D. Voici le maillage d'un octant de sphère avec une répartition des mailles uniformes selon le SimpleMesher1D et l'HybridDensityMesher1D :

SimpleMesher1D avec deux divisions sur chaque côté : 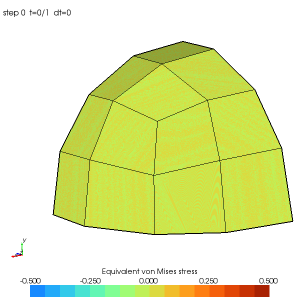HybridDensityMesher1D avec deux divisions sur chaque côté : 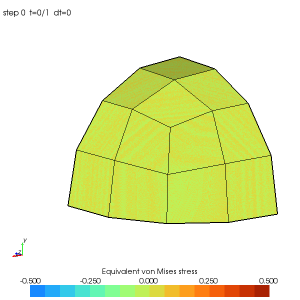Remarque : les trois sous-domaines sont égaux.

Article de référence : Hybrid Curve Point Distribution Algorithms, Khamayseh A. & Kuprat A., 2002.

Jusqu'à présent, les mailleurs transfinis implémentés dans Metafor ne permettent pas de traiter correctement le maillage d'une side ou d'un volume, lorsqu'un des bords de cette side ou de ce volume est discrétisé par une distribution de maille. L'implémentation de la nouvelle méthode est basée sur les pages 4-9 à 4-11 pour le mailleur transfini 2D et 4-44 à 4-45 pour le mailleur transfini 3D de la référence citée ci-dessous.

Désormais, il suffit de procéder de la manière suivante pour mailler une side ou un volume,

 MesherTFI2D =TransfiniteMesher2D(sideset(numero))
 MesherTFI2D.setEnableDistribution(True)
 MesherTFI2D.execute()
        
 MesherTFI3D =TransfiniteMesher3D(volset(numero))
 MesherTFI3D.setEnableDistribution(True)
 MesherTFI3D.execute()

lorsqu'un des bords d'une side ou d'un volume du maillage est discrétisé par une distribution de maille.

Remarque : Par défaut, le paramètre de la fonction setEnableDistribution est True.

Si on veut mailler la side suivante avec une distribution de maille, il est nécessaire d'activer la procédure de distribution de maille (Le rapport entre le dernier et le premier élément est de 10.) :

TFIMesher2D avec setEnableDistribution :

TFIMesher2D sans setEnableDistribution :

Bouquin de référence : Handbook of Grid Generation, Thompson J.F. , Soni K.S., Weatherill N.P. , 1999

Ajout des boîtes à outil pour générer un arc de cercle NURBS, une surface de révolution NURBS (oo_meta.toolbox.nurbsRevolutionSurface.py) et un patch sphérique NURBS (oo_meta.toolbox.nurbsSpheriquePatch.py).

Les fichiers python sont commentés pour chaque utilisation d'une fonction et/ou d'une classe, ainsi que des paramètres d'entrée et de sortie.

Puisque les NURBS peuvent représenter de manière exacte les coniques (parabole, ellipse, cercle, …) pour les courbes et les quadriques pour les surfaces (sphère, cylindre, …), cette boîte à outils pourrait être utiliser pour vérifier/valider les opérateurs de projection sur des NURBS.

Bouquin de référence : The NURBS Book (second edition, 1997), Les Piegl and Wayne Tiller.

Dans le fichier apps.toolbox.materialTesting, j'ai ajouté le paramètre “dtimeFactor” à passer au matériau dans le fichier exécutable .py du matériau pour pouvoir adapter le pas de temps maximum.

Grâce à ce paramètre-là, j'ai réussi à faire passer les matériaux suivants :

• GursonDamageNl8IH (dtimeFactor= 0.5)
• GursonDamageMoriTanakaLinearIH (dtimeFactor= 0.5)

Les matériaux qui posent encore des problèmes, sont les suivants :

• EvpIsoDamageLemaitre
• GursonViscoDamageMoriTanakaPowerIH
• GursonViscoDamagePowerIH
• NortonHoff2

Remarque :

Lorsque l'on impose dtimeFactor = 0.01 pour le matériau EvpIsoDamageLemaitre, les cas-tests considérés comme “Failed” (Trac2DEpeAnaSri, Trac2DEpeSNumSri et Trac2DEPeNumSri) tournent jusqu'au bout, mais par contre, les cas-tests (PureTrac2DKeepEpeNumEas et PureTrac3DKeepNumEas) ne tournent plus jusqu'au bout.

Pour chacun des matériaux problématiques, j'ai ajouté la possibilité de lancer les tests problématiques individuellement dans la fonction main du fichier exécutable .py :

Exemple NortonHoff2 :

def main() :

    testModule = pyutils.fileToModule(__file__, verb=False)
    if 1:
        testMat.execAll(NortonHoff2, testModule)  
    else:
        testMat.execOneAtChoice(NortonHoff2({'prpStiffMethod':STIFF_ANALYTIC,'cmvim':testMat.EAS()}), testMat.PlaneStrain(), CompresForce2DKeep())  
    print testModule, ' finished' 

Méthode du lagrangien augmenté :

• Débugger la méthode
• Nettoyage du code
• Ajout de nouveaux critères d'arrêt
• Implémentation des cas test de référence de l'article de J. C. Simo and T. A. Laursen, 1990
• Mettre à jour l'aire de contact nodale au cours des augmentations

[r]:
[a]:oo_meta\toolbox\nurbsRevolutionSurface.py
[a]:oo_meta\toolbox\nurbsSpheriquePatch.py
[a]:oo_meta\mtGeo\mtGeoHybridDensityMesher1D.cpp
[a]:oo_meta\mtGeo\mtGeoHybridDensityMesher1D.h

[r]:
[a]:

— Gaëtan WAUTELET 2013/06/14