L'élément AEJ (“Average Elemental Jacobian”) est un élément triangle ou tétra de degré 1, qui permet d'éviter le locking de la formulation standard dans des situations d'incompressibilité ( coefficient de Poisson proche de 0.5, mais aussi plasticité de Von Mises ).

Il est appelé comme suit, en 2D:

   prp = ElementProperties(TriangleAej2DElement)
   prp.put (CAUCHYMECHVOLINTMETH, VES_CMVIM_AEJ)

et en 3D:

   prp = ElementProperties(TriangleAej3DElement)
   prp.put (CAUCHYMECHVOLINTMETH, VES_CMVIM_AEJ)     

Il peut être utilisé à la fois pour les matériaux hypo ( élasticité linéaire, élasto-plasticité) et pour les matériaux hyper (hyperélastiques)

Pour plus de détails: cfr. ma thèse http://hdl.handle.net/2268/136159

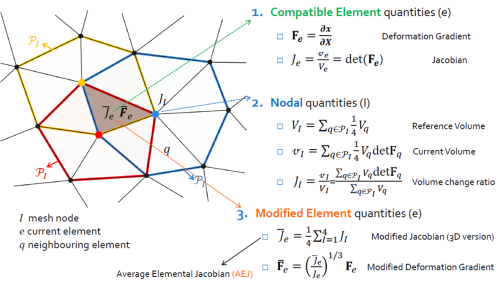
Le principe de l'élément AEJ est de remplacer le Jacobien J_e 'cinématique' de l'élément, qui donne le taux de compression de cet élément, par une nouvelle valeur, appelée J_e,barre . Ce Jacobien modifié est obtenu en: (1) définissant des Jacobiens nodaux J_I (2) moyennant les J_I sur l'élément. Ceci revient en fait à imposer les contraintes d'incompressibilité aux noeuds et non plus au point de Gauss de l'élément.

Les ddls de l'élément AEJ sont donc étendus: ils correspondent aux ddls de l'élément tri ou tet standard, additionnés aux ddls des noeuds voisins.

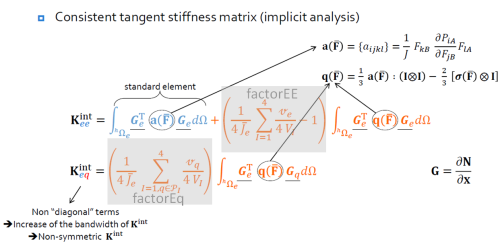
C'est pourquoi il apparaît dans la matrice de raideur des termes liant les noeuds de l'élément tri ou tet e avec les noeuds de l'élément voisin q. La matrice de raideur analytique est calculée comme suit:

Le dossier mtElements/aej reprend les différentes routines relatives à ce nouvel élément. Ce dossier est similaire à mtElements/volumes.

L'élément AEJ triangulaire 2D est défini dans TriangleAej2DElement et le tétraèdre AEJ 3D dans TetraAej3DElement, tous deux dérivent de AEJElement.

Les noeuds et ddls sont classés en Level1 (les trois (en 2D) ou quatre (en 3D) noeuds centraux dans l'image ci-dessus) et Level2 (le noeuds provenant des voisins).

Dans AejElement_mec, on a une fonction initialiseAejProperties, appelée en début de calcul, qui calcule le voisinage; et une fonction updateAejProperties, qui calcule à chaque pas de temps, le nouvel J_e,barre de l'élément (utilisé dans le computeStrains()), ainsi que les nouveaux factorEE et les factorEQ (cfr. image ci-dessus) correspondants (utilisé pour l'update de la matrice de raideur).

Ensuite, nous avons les deux méthodes StdCauchyMechAejIntegMeth pour l'hypo et Pk2MechAejIntegMeth pour l'hyper. Dans ces routines, nous avons deux modifications principales par rapport aux routines classiques de l'élément volumique:

1. computeStrains() est appelé avec une matrice Jacobienne modifiée, de telle manière à ce que sont déterminant soit le nouveau J_e,barre de la méthode AEJ
2. fillMechanicalAnalyticalStiffness() reprend le calcul de la matrice de raideur analytique via la formule de l'image ci-dessus.

La classe LoadMesh qui permet typiquement de charger un maillage vtkUnstructuredGrid dans Metafor a été modifiée de manière à pouvoir également charger un maillage volumique hexahédrique. Idéalement le nom du fichier tetgen.py devrait être changé en quelque chose de plus général (vtkmeshingTools.py ?)

• Dossier oo_meta\apps\aej
• Dossier oo_meta\mtElements\aej

— — Vinciane d'Otreppe 2013/02/15 15:01